Как построить линию уровней
- Линии уровня функции и их применение в различных областях
- Построение линий уровня
- Приведение функции к виду f(x,y) = const
- Построение линий уровня
- Использование сервисов для построения линий уровня
Линии уровня функции и их применение в различных областях
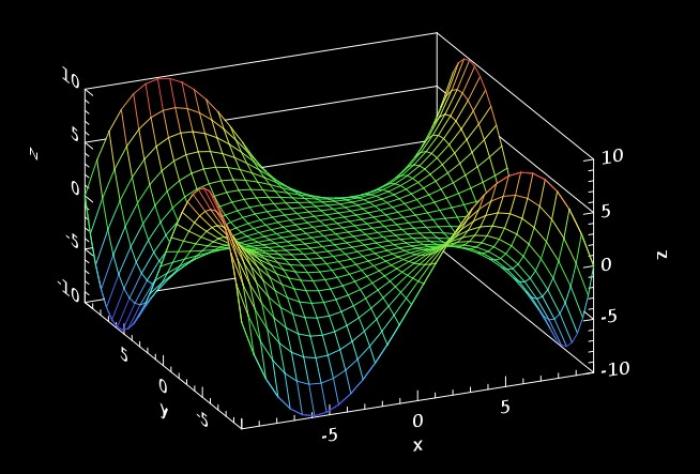
Линией уровня функции называется множество точек пространства, в которых функция принимает одинаковые значения. Эти линии могут быть использованы в различных областях, таких как математика, физика, картография и метеорология.
Построение линий уровня
Для построения линий уровня исходят из того, что они являются проекциями на плоскость с нулевой аппликатой линий пересечения графика функции с горизонтальной плоскостью. Аппликата - это константа, к которой приравнивается уравнение функции, чтобы получить координаты точек линии. Шаг аппликаты может меняться в зависимости от заданных условий задачи. Если требуется построить только одну линию уровня, то условия могут указывать координаты точки на этой линии.
Приведение функции к виду f(x,y) = const
Заданную функцию нужно привести к виду f(x,y) = const. Например, можно привести функцию z = x² + y² - 4*y к виду c+4 = x²+(y-2)². Такая функция представляет собой бесконечный параболоид, а линии уровня являются концентрическими кругами с радиусом, определяемым по формуле √(c+4).
Построение линий уровня
Для построения линий уровня нужно подставить значение константы c, заданное в условиях задачи или выбранное в соответствии с областью значений функции. Если требуется построить несколько линий уровня, то повторяют предыдущий шаг нужное число раз.
Использование сервисов для построения линий уровня
В интернете можно найти сервисы, которые помогут с построением линий уровней. Например, сервис WolframAlpha предоставляет возможность ввести формулу функции и получить двух- и трехмерные графики с линиями уровней. Этот сервис также предоставляет классификацию фигуры, описываемой функцией, альтернативные формы записи и другие свойства функции, которые могут быть полезны при построении линий уровней.