Как найти диагональ четырехугольника
- Как найти диагональ четырехугольника?
- Прямоугольник и его диагонали
- Параллелограмм и его диагонали
- Трапеция и ее диагонали
Как найти диагональ четырехугольника?
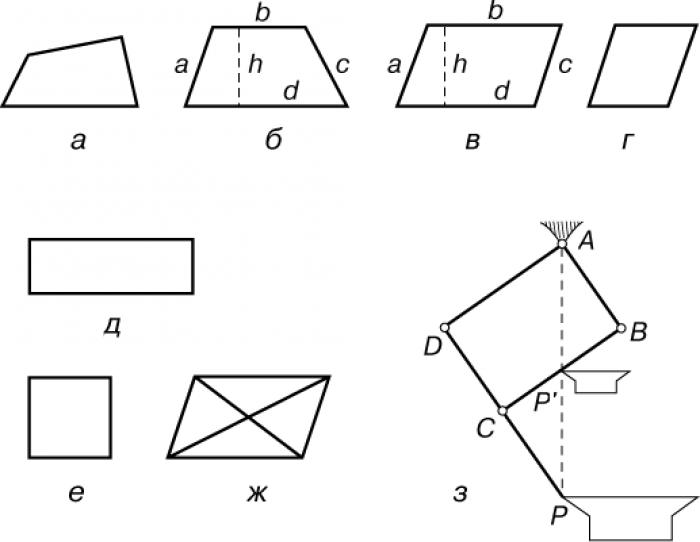
Четырехугольник - это геометрическая фигура, состоящая из четырех сторон и углов, прилегающих к ним. В задачах по геометрии часто требуется найти диагональ одной из этих фигур. Давайте рассмотрим несколько методов для нахождения диагонали различных четырехугольников.
Прямоугольник и его диагонали
Прямоугольник - это частный случай четырехугольника, у которого все углы прямые. Его диагонали равны, пересекаются в одной точке и делятся пополам. Если известны две стороны прямоугольника, то его диагонали можно найти с помощью формулы: d1 = √a^2 + b^2 = d2, где a и b - стороны прямоугольника, d1 и d2 - его диагонали.
Если рассматривать квадрат - частный случай прямоугольника, у которого все стороны равны, то его диагональ будет равна a√2, где a - длина стороны.
Также можно найти диагональ прямоугольника, зная его площадь. Формула для этого выглядит следующим образом: d = √2S, где S - площадь квадрата или прямоугольника.
Параллелограмм и его диагонали
Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны. В отличие от прямоугольника или квадрата, у параллелограмма не все углы равны, а только противоположные.
Если в задаче дан параллелограмм со сторонами a и b и углом между ними, то его диагональ можно найти с помощью теоремы косинусов: d^2 = a^2 + b^2 - 2ab*cosα, где d - диагональ параллелограмма, α - угол между сторонами.
Ромб - это параллелограмм, у которого все стороны равны. Если в задаче требуется найти диагональ ромба, то потребуются значения его второй диагонали и площади. Формула для вычисления второй диагонали выглядит следующим образом: d2 = 2S/d1, где S - площадь ромба, d1 и d2 - его диагонали.
Трапеция и ее диагонали
Трапеция - это четырехугольник, у которого две стороны параллельны, а две другие - нет. Для вычисления диагонали трапеции может понадобиться использование тригонометрических функций.
Если трапеция является равнобочной и известны ее первая диагональ d1 и угол между двумя диагоналями, то вторую диагональ можно найти по формуле: d2 = 2S/d1*sinφ, где φ - угол между диагоналями.
Если рассматривать прямоугольную трапецию, у которой одна из сторон совпадает с высотой, а также известно нижнее основание, то диагональ можно найти с помощью теоремы Пифагора: d = √(a^2 + b^2), где a и b - стороны трапеции.
В зависимости от типа четырехугольника, существуют различные способы нахождения его диагонали. Используя формулы и теоремы, описанные выше, можно эффективно решать задачи по геометрии, связанные с нахождением диагонали четырехугольника.