Как привести дроби к общему знаменателю
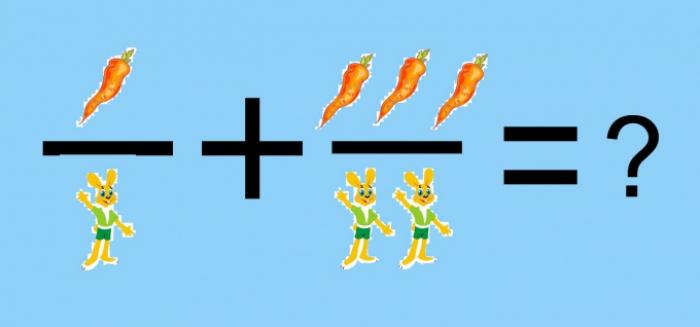
- Приведение дробей к общему знаменателю: инструкция
- Понятия числителя и знаменателя
- Понятие кратного, суммы и разности
- Понятие расширения дробей
- Инструкция по приведению дробей к общему знаменателю:
- Сравнение дробей с разными знаменателями
- Вывод
Приведение дробей к общему знаменателю: инструкция
Необходимость привести дроби к общему знаменателю возникает, когда нужно найти их сумму или разность. Общий знаменатель также необходим для сравнения дробей.
Понятия числителя и знаменателя
Перед приступлением к приведению дробей к общему знаменателю, важно понять, что числитель в дроби обозначает количество частей или долю, а знаменатель указывает на количество равных частей в целом.
Понятие кратного, суммы и разности
Для приведения дробей к общему знаменателю необходимо понимать понятие кратного числа, а также умение находить сумму и разность дробей.
Понятие расширения дробей
Расширение дробей - это процесс, при котором мы умножаем числитель и знаменатель дроби на одно и то же число, чтобы получить эквивалентную дробь с новым знаменателем.
Инструкция по приведению дробей к общему знаменателю:
- Возьмите две дроби с разными знаменателями. Обозначьте их как a/x и b/y.
- Найдите наименьшее общее кратное для заданных знаменателей (НОК(x, y)).
- Вычислите дополнительный множитель для каждой дроби. Для дроби a/x он будет равен НОК(x, y) деленному на знаменатель x.
- Аналогично вычислите значение дополнительного множителя для второй дроби, используя формулу n = НОК(x, y) / y.
- Умножьте числители и знаменатели обеих дробей на соответствующие дополнительные множители.
- Полученные дроби a*m/x*m и b*n/y*n будут иметь один и тот же знаменатель, равный x*m = y*n.
Сравнение дробей с разными знаменателями
Если необходимо сравнить несколько дробей с разными знаменателями, необходимо найти наименьшее общее кратное для всех знаменателей.
Вывод
Приведение дробей к общему знаменателю является необходимым для нахождения их суммы или разности, а также для сравнения дробей. Следуя инструкции, можно легко привести дроби к общему знаменателю и провести необходимые операции.
Перед решением примеров на сложение и вычитание дробей, рекомендуется освежить память о свойствах простых дробей.