Как разделить окружность на 12 частей
- Геометрические построения и их важность в обучении
- Простые и сложные задачи на построения
- Инструкция по построению окружности и разделению ее на части
- Полезные советы
Геометрические построения и их важность в обучении
Геометрические построения являются неотъемлемой частью программы обучения и играют важную роль в развитии воображения, логики и пространственного мышления. Они помогают закрепить восприятие зависимостей между параметрами геометрических объектов, развивая при этом умение решать задачи с помощью линейки, циркуля и карандаша.
Простые и сложные задачи на построения
Большинство задач на построения достаточно простые и естественные, такие как построение диагоналей квадрата или равнобедренного треугольника. Однако, некоторые задачи требуют более глубокого анализа и тщательного планирования. К примеру, разделение окружности на 12 равных частей требует некоторой мыслительной активности.
Инструкция по построению окружности и разделению ее на части
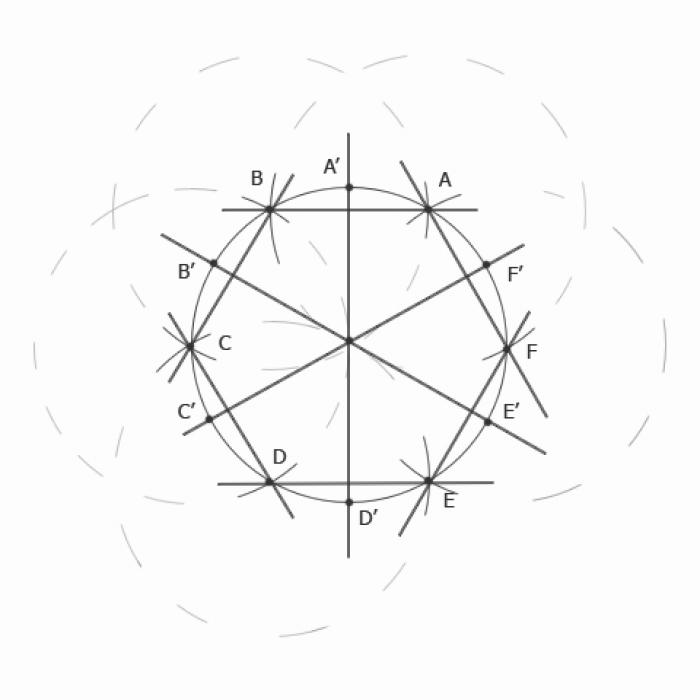
1. Нарисуйте окружность, либо найдите радиус существующей окружности, используя линейку, циркуль и карандаш.
2. Разделите окружность на шесть частей, перемещая ножку циркуля и рисуя дуги, пока не найдете шесть точек, делящих окружность на равные части.
3. Постройте правильный шестиугольник, соединяя найденные точки A, B, C, D, E, F.
4. Для разделения окружности на двенадцать частей, постройте перпендикуляры к отрезкам между точками A, B, C и D на окружности. Точки пересечения данных перпендикуляров с окружностью будут точками разделения.
Полезные советы
- Будьте внимательны при работе с циркулем, не меняйте расстояние между его ножками в процессе построений.
- Используйте металлическую линейку и твердый карандаш для более точных и аккуратных построений.
Геометрические построения являются важным аспектом обучения и способствуют развитию различных навыков. Они помогают студентам развить воображение, логику и пространственное мышление. Большинство задач на построения решаются с помощью линейки, циркуля и карандаша, что позволяет закрепить восприятие зависимостей между параметрами геометрических объектов.
Некоторые построения, такие как диагонали квадрата или равнобедренный треугольник, не составляют особого труда. Однако, более сложные задачи, например разделение окружности на 12 равных частей, требуют более глубокого анализа и тщательного планирования.
Для построения окружности и разделения ее на части необходимы линейка, циркуль и карандаш. Сначала рисуется окружность или находится радиус существующей. Затем, с помощью циркуля и линейки, окружность разделяется на шесть равных частей. Найденные точки соединяются линиями, чтобы построить правильный шестиугольник. Для разделения окружности на двенадцать равных частей, строятся перпендикуляры к отрезкам, соединяющим точки на окружности.
При работе с циркулем важно не менять расстояние между его ножками в процессе построений, чтобы сохранить точность и правильность результата. Использование металлической линейки и твердого карандаша также способствует точности и аккуратности построений.
Геометрические построения являются не только важной частью обучения, но и увлекательным способом развития навыков решения задач, абстрактного мышления и творческого подхода к решению проблем.