Как решить квадратное неравенство
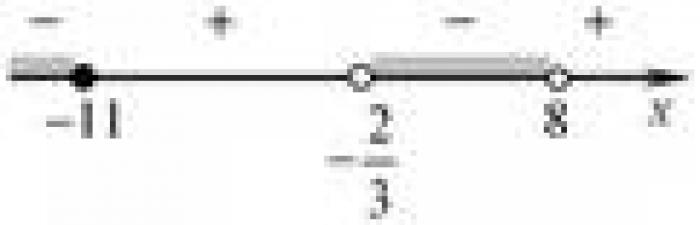
- Решение квадратных неравенств методом интервалов
- Умение решать квадратные уравнения
- Применение метода интервалов
- Поиск решений
- Полезные советы
Решение квадратных неравенств методом интервалов
Решение квадратных неравенств и уравнений является важной частью учебного курса алгебры. Это навык, который пригодится не только для сдачи Единого Государственного Экзамена по математике, но и при поступлении в высшее учебное заведение. Хоть это может показаться сложным, разобраться в решении квадратных неравенств довольно просто. Существует несколько алгоритмов, одним из наиболее простых из которых является метод интервалов. Следуя этому методу, можно последовательно прийти к решению неравенства.
Умение решать квадратные уравнения
Для того чтобы решить квадратное неравенство методом интервалов, сначала необходимо решить соответствующее квадратное уравнение. Переносим все члены уравнения с переменной и свободный член в левую часть, а в правой остается ноль. Корни квадратного уравнения, соответствующего неравенству (с знаком "больше" или "меньше" замененным на "равно"), можно найти используя известные формулы через дискриминант.
Применение метода интервалов
На втором этапе записываем неравенство в виде произведения двух скобок (x - x1)(x - x2) ≠ 0. Затем отмечаем найденные корни на числовой оси. После этого смотрим на знак неравенства. Если неравенство строгое ("больше" или "меньше"), то точки, которыми отмечены корни на числовой оси, являются пустыми. В противном случае ("больше или равно") точки отмечаются на числовой оси.
Поиск решений
Далее, выбираем число, которое находится левее первого (или правее на числовой оси) корня. Если при подстановке этого числа в неравенство оно оказывается верным, то интервал от "минус бесконечности" до самого малого корня является одним из решений уравнения, наравне с интервалом от второго корня до "плюс бесконечности". В противном случае, решением будет интервал между корнями.
Полезные советы
При решении соответствующего квадратного уравнения не допускайте ошибок, иначе вы можете неправильно решить неравенство. Также не забывайте о том, строгое или нестрогое неравенство решаете. Если неравенство строгое, то используйте круглые скобки (не берите в интервал корень уравнения), иначе используйте квадратные скобки.