Как решить систему с тремя неизвестными
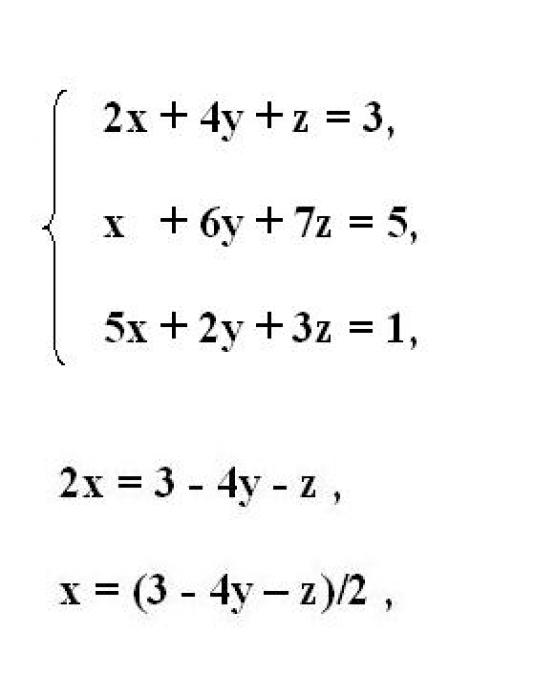
- Способы решения линейной системы с тремя неизвестными
- Метод подстановки
- Инструкция по решению системы уравнений третьего порядка
- 1. Запишите исходную систему уравнений третьего порядка.
Способы решения линейной системы с тремя неизвестными
Линейная система с тремя неизвестными имеет несколько способов решения. Найти решение системы можно с помощью правила Кремера через определители, методом Гаусса или используя простой способ подстановки.
Метод подстановки
Метод подстановки является основным для решения систем линейных уравнений небольшого порядка. Он заключается в поочередном выражении из каждого уравнения системы одной неизвестной переменной, подстановке ее в следующее уравнение и упрощение получаемых выражений.
Инструкция по решению системы уравнений третьего порядка
1. Запишите исходную систему уравнений третьего порядка.
2. Из первого уравнения системы выразите первую неизвестную переменную х. Для этого перенесите члены, содержащие другие переменные, за знак равенства. Перенесенным членам поменяйте знак на противоположный.
3. Если при множителе с выражаемой переменной присутствует коэффициент, отличный от единицы, поделите на его значение все уравнение. Таким образом, вы получите переменную х, выраженную через остальные члены уравнения.
4. Подставьте во второе уравнение вместо х то выражение, которое вы получили из первого уравнения. Упростите полученную запись, произведя сложение или вычитание подобных членов. Аналогично предыдущему шагу выразите из второго уравнения следующую неизвестную переменную у. Также перенесите все другие члены за знак равенства и поделите все уравнение на коэффициент при у.
5. В последнее третье уравнение подставьте вместо двух неизвестных переменных х и у выраженные значения из первого и второго уравнений системы. Причем в выражении х также замените переменную у. Упростите полученное уравнение. В нем в качестве неизвестной величины останется лишь третья переменная z. Выразите ее из уравнения, как описано выше, и высчитайте ее значение.
6. В выражение у из второго уравнения подставьте известное значение переменной z. Подсчитайте значение переменной у. Далее в выражение переменной х подставьте значения переменных у и z. Вычислите х. Запишите полученные значения х, у и z – это и есть решение системы с тремя неизвестными.