Как составить каноническое уравнение прямой
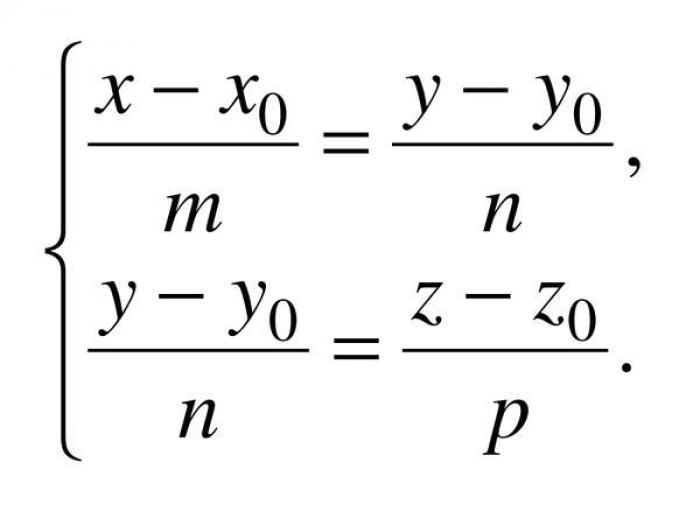
- Прямая в геометрии
- Графическое представление прямой
- Аналитическое определение прямой
- Каноническое уравнение прямой
- Каноническое уравнение прямой в пространстве
Прямая в геометрии
Прямая является одним из основных понятий геометрии. Она может быть представлена аналитически с помощью уравнений или системы уравнений на плоскости или в пространстве.
Графическое представление прямой
Графически прямая изображается в виде линии, у которой концы неограничены. Хотя прямую нельзя изобразить полностью на графике, схематическое изображение предполагает, что прямая продолжается в бесконечность в обе стороны. Прямую обозначают строчными латинскими буквами, например, a или c.
Аналитическое определение прямой
Аналитически прямая в плоскости задается уравнением первой степени, а в пространстве - системой уравнений. Существуют различные виды уравнений прямой, такие как общее, нормальное, параметрическое, векторно-параметрическое, тангенциальное и каноническое уравнения через декартову систему координат.
Каноническое уравнение прямой
Каноническое уравнение прямой является результатом преобразования параметрических уравнений. Параметрические уравнения прямой записываются в виде X = x_0 + a*t и y = y_0 + b*t, где x_0 и y_0 - координаты некоторой точки принадлежащей прямой, a и b - координаты направляющего вектора прямой, а t - параметр, который определяет положение точки N на прямой.
Каноническое уравнение прямой в пространстве
Каноническое уравнение прямой в пространстве задается тремя координатами и имеет вид (x - x_0)/a = (y - y_0)/b = (z - z_0)/c, где x_0, y_0 и z_0 - координаты точки принадлежащей прямой, a, b и c - координаты направляющего вектора прямой. Кроме того, a^2 + b^2 + c^2 должно быть неравно нулю.






