Как составить уравнения сторон треугольника
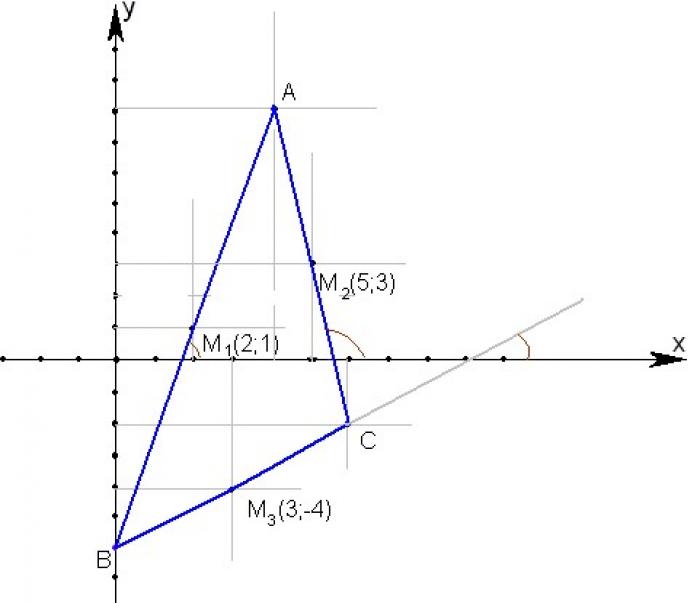
- Определение треугольника по координатам вершин
- Шаг 1: Задание координат точек
- Шаг 2: Проверка различности точек
- Шаг 3: Нахождение уравнения прямой через две точки
- Шаг 4: Вычисление углового коэффициента
- Шаг 5: Вычисление смещения
- Шаг 6: Проверка точек на принадлежность прямой
- Шаг 7: Повторение процесса для остальных сторон
- Окончательные уравнения для сторон треугольника
Определение треугольника по координатам вершин
В аналитической геометрии одним из способов определения треугольника является задание координат трех его вершин. Эти координаты позволяют однозначно определить треугольник, однако для полноты картины необходимо составить уравнения сторон, соединяющих вершины.
Шаг 1: Задание координат точек
Для начала, нам заданы координаты трех точек (x1, y1), (x2, y2), (x3, y3), предполагая, что эти точки являются вершинами треугольника. Задача состоит в составлении уравнений для его сторон, то есть уравнений прямых, на которых лежат эти стороны. Уравнения должны иметь вид y = kx + b, где k и b - угловые коэффициенты и смещения соответственно.
Шаг 2: Проверка различности точек
Перед составлением уравнений следует убедиться, что все три точки различны между собой. Если какие-то две точки совпадают, треугольник вырождается в отрезок.
Шаг 3: Нахождение уравнения прямой через две точки
Для начала найдем уравнение прямой, проходящей через точки (x1, y1) и (x2, y2). Если x1 = x2, то прямая будет вертикальной и ее уравнение будет x = x1. Если y1 = y2, то прямая будет горизонтальной и ее уравнение будет y = y1. В общем случае, когда координаты не равны друг другу, уравнение прямой можно записать в виде y = kx + b.
Шаг 4: Вычисление углового коэффициента
Подставляя координаты (x1, y1) и (x2, y2) в уравнение прямой, получаем систему из двух линейных уравнений: k1*x1 + b1 = y1 и k1*x2 + b1 = y2. Вычитая одно уравнение из другого, можно решить полученное уравнение относительно k1: k1*(x2 - x1) = y2 - y1. Следовательно, угловой коэффициент k1 равен (y2 - y1)/(x2 - x1).
Шаг 5: Вычисление смещения
Подставляя найденное выражение для k1 в любое из исходных уравнений, можно найти выражение для b1: ((y2 - y1)/(x2 - x1))*x1 + b1 = y1. Раскрывая скобки и упрощая, получаем b1 = (x1*y2 - x2*y1)/(x2 - x1). Если уже известно, что x2 ≠ x1, выражение можно дополнительно упростить.
Шаг 6: Проверка точек на принадлежность прямой
Для проверки того, лежит ли третья заданная точка на найденной прямой, необходимо подставить значения (x3, y3) в уравнение прямой и проверить равенство. Если равенство выполняется, значит, все три точки лежат на одной прямой, и треугольник вырождается в отрезок.
Шаг 7: Повторение процесса для остальных сторон
Аналогичным образом, можно получить уравнения для прямых, проходящих через точки (x2, y2), (x3, y3) и (x1, y1), (x3, y3).
Окончательные уравнения для сторон треугольника
Таким образом, окончательные уравнения для сторон треугольника, заданного координатами его вершин, будут иметь вид:
(1) y = ((y2 - y1)*x + (x1*y2 - x2*y1))/(x2 - x1);
(2) y = ((y3 - y2)*x + (x2*y3 - x3*y2))/(x3 - x2);
(3) y = ((y3 - y1)*x + (x1*y3 - x3*y1))/(x3 - x1).






