Как упростить выражение
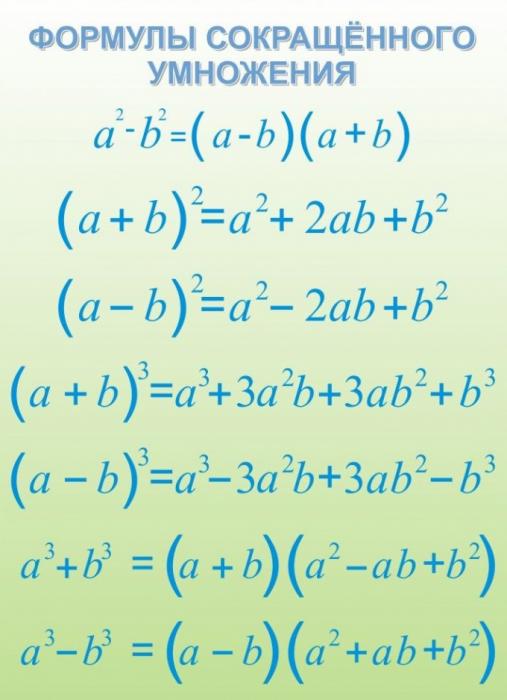
- Упрощение математических выражений: основные приемы и формулы
- Сокращение одночленов
- Использование формул сокращенного умножения
- Сокращение дробей
- Свод одночленов с одинаковыми степенями
- Упрощение тригонометрических выражений
- Вывод
Упрощение математических выражений: основные приемы и формулы
Чтобы быстро и эффективно производить расчеты, необходимо упрощать математические выражения. Для этого можно использовать различные математические соотношения, которые позволят сделать выражение короче и расчеты более простыми.
Сокращение одночленов
Если в выражении имеются одночлены с одинаковыми множителями, то можно найти их сумму коэффициентов и умножить на единый для них множитель. Например, если есть выражение 2•а-4•а+5•а+а, то можно вынести общий множитель а и получить (2-4+5+1)∙а=4∙а.
Использование формул сокращенного умножения
Для упрощения выражений можно использовать формулы сокращенного умножения, такие как квадрат разности, разность квадратов и разность и сумма кубов. Например, если есть выражение 256-384+144, то его можно представить как 16²-2•16•12+12²=(16-12)²=4²=16.
Сокращение дробей
Если выражение представляет собой натуральную дробь, то можно выделить общий множитель из числителя и знаменателя и сократить дробь на него. Например, если нужно сократить дробь (3•a²-6•a•b+3•b²)/(6∙a²-6∙b²), то можно вынести общие множители из числителя и знаменателя и получить выражение (a-b)²/(2∙ (a+b)∙(a-b)). Затем можно сократить числитель и знаменатель на (a-b) и получить (a-b)/(2∙ (a+b)), что гораздо легче посчитать при конкретных значениях переменных.
Свод одночленов с одинаковыми степенями
Если одночлены имеют одинаковые множители, возведенные в степень, то при их суммировании необходимо следить, чтобы степени были равны, иначе сводить подобные нельзя. Например, если есть выражение 2∙m²+6•m³-m²-4•m³+7, то при сведении подобных получится m²+2•m³+7.
Упрощение тригонометрических выражений
При упрощении тригонометрических выражений можно использовать различные формулы для их преобразования. Например, основное тригонометрическое тождество sin²(x)+cos²(x)=1 может быть использовано для упрощения выражений. Также можно использовать формулы суммы и разности аргументов, двойного и тройного аргумента и другие.
Например, рассмотрим выражение (sin(2∙x)- cos(x))/ ctg(x). Можно распиать формулу двойного аргумента и котангенса, как отношение косинуса на синус, и получить (2∙ sin(x)• cos(x)- cos(x))• sin(x)/cos(x). Затем можно вынести общий множитель cos(x) и сократить дробь cos(x)•(2∙ sin(x) - 1)• sin(x)/cos(x)= (2∙ sin(x) - 1) • sin(x).
Вывод
Упрощение математических выражений - важный навык, который позволяет производить расчеты быстро и эффективно. Используя различные математические соотношения и формулы, можно значительно упростить выражения и сделать расчеты более простыми. Чтобы успешно использовать эти приемы, необходимо хорошо знать основные понятия и теоретические сведения, связанные с математическими соотношениями и формулами.