Как вычислить площадь фигуры, ограниченной графиками функций

- Вычисление площади фигуры, ограниченной графиками двух функций
- Построение графиков и вычисление площади фигуры
- Пример вычисления площади замкнутой фигуры
- Решение примера
- Другой пример вычисления площади замкнутой фигуры
- Решение примера
Вычисление площади фигуры, ограниченной графиками двух функций
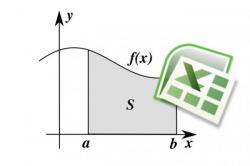
Графики двух функций на общем интервале образуют определенную фигуру. Чтобы вычислить ее площадь, необходимо проинтегрировать разность функций. Границы общего интервала могут быть заданы изначально или являться точками пересечений двух графиков.
Построение графиков и вычисление площади фигуры
При построении графиков двух заданных функций в области их пересечения образуется замкнутая фигура, ограниченная этими кривыми и двумя прямыми линиями х=а и х=b, где а и b – концы рассматриваемого интервала. Эту фигуру визуально отображают штрихом. Ее площадь можно вычислить, проинтегрировав разность функций.
Функция, расположенная выше на графике, является большей величиной, следовательно, в формуле ее выражение будет стоять первым: S = ∫f1 – ∫f2, где f1 > f2 на промежутке [а, b]. Впрочем, приняв во внимание, что количественная характеристика любого геометрического объекта является величиной положительной, можно вычислить площадь фигуры, ограниченной графиками функций, по модулю: S = |∫f1 – ∫f2|.
Такой вариант тем более удобен, если нет возможности или времени на построение графика. При вычислении определенного интеграла пользуются правилом Ньютона-Лейбница, которое предполагает подстановку в конечный результат предельных значений интервала. Тогда площадь фигуры равна разности двух значений первообразной, найденной на этапе интегрирования, из большего F(b) и меньшего F(a).
Пример вычисления площади замкнутой фигуры
Иногда замкнутая фигура на заданном интервале образуется путем полного пересечения графиков функций, т.е. концы интервала являются точками, принадлежащими обеим кривым. Например: найдите точки пересечения линий у = х/2 + 5 и у = 3•х – х²/4 + 3 и вычислите площадь.
Решение примера
Чтобы найти точки пересечения, составьте уравнение: х/2 + 5 = 3•х – х²/4 + 3 → х² – 10•х + 8 = 0D = 100 - 64 = 36 → х1,2 = (10 ± 6)/2. Итак, вы нашли концы интервала интегрирования [2; 8]: S = |∫ (3•х – х²/4 + 3 – х/2 - 5)dх| = |(5•х²/4 – х³/12 - 2•х)| ≈ 59.
Другой пример вычисления площади замкнутой фигуры
Рассмотрим другой пример: у1 = √(4•х + 5); у2 = х и дано уравнение прямой х = 3. В этой задаче дан только один конец интервала х=3. Это значит, что второе значение требуется найти из графика. Постройте линии, заданные функциями у1 и у2. Очевидно, что значение х=3 является верхним ограничением, следовательно, нужно определить нижний предел. Для этого приравняйте выражения: √(4•х + 5) = х ↑²4•х + 5 = х² → х² – 4•х – 5 = 0.
Решение примера
Найдите корни уравнения: D = 16 + 20 = 36 → х1 = 5; х2 = -1. Посмотрите на график, нижним значением интервала является -1. Поскольку у1 расположено выше у2, то: S = ∫(√(4•х + 5) - х)dх на промежутке [-1; 3]. S = (1/3•√((4•х + 5)³) – х²/2) = 19.