Как вычислить радиус вписанной окружности в треугольник
- Вычисление радиуса вписанной окружности в треугольнике
- Вычисление радиуса с помощью длин сторон
- Вычисление радиуса с помощью площади треугольника
- Вычисление радиуса с помощью длины стороны, угла и периметра
- Вычисление радиуса в прямоугольном треугольнике
- Вычисление радиуса в правильном треугольнике
Вычисление радиуса вписанной окружности в треугольнике
В треугольнике можно вписать окружность, которая будет касаться каждой стороны только в одной точке. Радиус этой окружности зависит от параметров треугольника, таких как длины сторон, величины углов, площадь и периметр. Для вычисления радиуса вписанной окружности не обязательно знать все параметры треугольника.
Вычисление радиуса с помощью длин сторон
Если известны длины всех сторон треугольника (a, b и c), для вычисления радиуса (r) вписанной окружности необходимо сначала добавить переменную полупериметра (p). Полупериметр вычисляется как половина суммы длин всех сторон: p = (a+b+c)/2.
Формула для вычисления радиуса вписанной окружности будет содержать знак радикала, под которым находится дробь с полупериметром в знаменателе. В числителе этой дроби необходимо умножить разность полупериметра на разности между полупериметром и длинами каждой из сторон: r = √((p-a)*(p-b)*(p-c)/p).
Вычисление радиуса с помощью площади треугольника
Если помимо длин сторон (a, b и c) известна площадь треугольника (S), радиус вписанной окружности (r) можно вычислить без извлечения корня. Удвойте площадь и разделите результат на сумму длин всех сторон: r = 2*S/(a+b+c). Если ввести полупериметр (p = (a+b+c)/2), формула для вычисления радиуса будет гораздо проще: r = S/p.
Вычисление радиуса с помощью длины стороны, угла и периметра
Если известны длина одной из сторон треугольника (a), величина лежащего напротив него угла (α) и периметр (P), для вычисления радиуса вписанной окружности можно использовать тригонометрическую функцию - тангенс. Формула для вычисления радиуса будет содержать разность между половиной периметра и длиной стороны, умноженную на тангенс половины величины угла: r = (P/2-a)*tg(α/2).
Вычисление радиуса в прямоугольном треугольнике
В прямоугольном треугольнике с известными длинами катетов (a и b) и гипотенузы (c) радиус вписанной окружности (r) вычисляется просто. Сложите длины катетов, вычтите из результата длину гипотенузы и поделите полученную величину пополам: r = (a+b-c)/2.
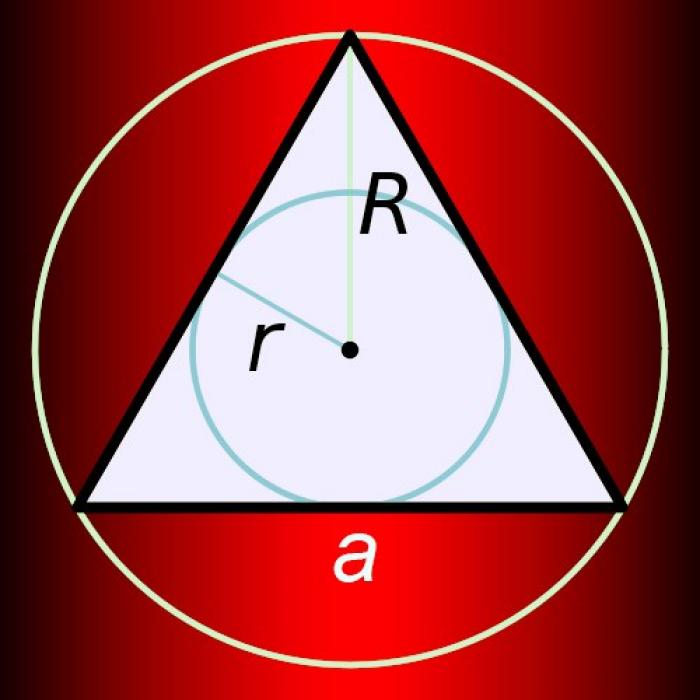
Вычисление радиуса в правильном треугольнике
Радиус окружности (r), вписанной в правильный треугольник с известной длиной стороны (a), может быть вычислен по простой формуле. Умножьте длину стороны на бесконечную дробь, в числителе которой стоит корень из тройки, а в знаменателе - шестерка: r = a*√3/6.
Теперь, зная различные способы вычисления радиуса вписанной окружности в треугольнике, можно выбрать подходящую формулу в зависимости от известных параметров.