Как вычислить сторону равнобедренного треугольника
- Равнобедренный треугольник и его параметры
- Вычисление длины боковой стороны по известным данным
- Вычисление длины основания по заданным данным
- Вычисление длины сторон при наличии описанной окружности
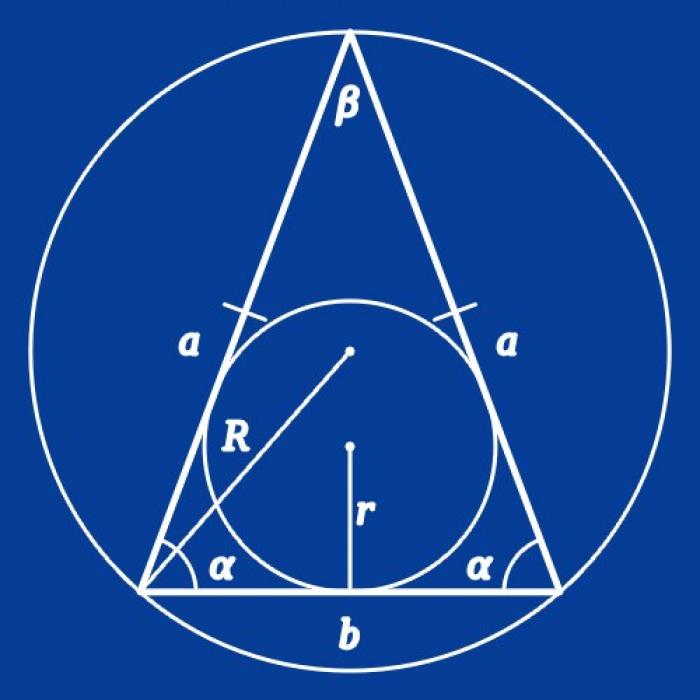
Равнобедренный треугольник и его параметры
Равнобедренным треугольником называется треугольник, у которого две стороны имеют одинаковую длину. Для вычисления длины сторон такой фигуры можно использовать знание углов в его вершинах и другие параметры, такие как длина стороны или радиус описанной окружности. В данной статье рассмотрим различные методы вычисления длины сторон равнобедренного треугольника.
Вычисление длины боковой стороны по известным данным
Для вычисления длины боковой стороны равнобедренного треугольника (b) по известной длине основания (a) и величине прилегающего к нему угла (α), можно использовать теорему косинусов. Формула для вычисления стороны b будет следующей: b = a / (2 * cos(α)).
Ту же теорему можно использовать и для обратной операции - вычисления длины основания (a) по известной длине боковой стороны (b) и величине угла (α). В этом случае формула будет выглядеть следующим образом: a = 2 * b * cos(α).
Вычисление длины основания по заданным данным
Если кроме длин боковых сторон (b) в условиях задачи также указана величина угла между ними (β), для расчета длины основания (a) можно воспользоваться теоремой синусов. Формула для вычисления длины основания будет следующей: a = 2 * b * sin(β/2).
Теорему синусов можно использовать и для нахождения длины боковой стороны (b) равнобедренного треугольника, если известна длина основания (a) и величина противолежащего ему угла (β). В этом случае формула будет следующей: b = a / (2 * sin(β/2)).
Вычисление длины сторон при наличии описанной окружности
Если около равнобедренного треугольника описана окружность, радиус которой (R) известен, для вычисления длин сторон нужно знать величину угла в одной из вершин фигуры. Если в условиях указан угол между боковыми сторонами (β), то для вычисления длины основания (a) следует использовать формулу: a = 2 * R * sin(β).
Если же дана величина угла при основании (α), то для вычисления длины боковой стороны (b) применяется формула: b = 2 * R * sin(α).
В заключение, равнобедренный треугольник имеет ряд характеристик и параметров, которые могут быть вычислены с использованием различных формул. Знание этих формул позволяет решать задачи по вычислению длины сторон треугольника при известных углах или других параметрах.