Как найти длину окружности, зная ее радиус
- Окружность и ее радиус
- Анализ данных
- Вычисление длины окружности
- Пример
- Окружность в многоугольниках
- Окружность в треугольнике и четырехугольнике
- Использование трафаретов
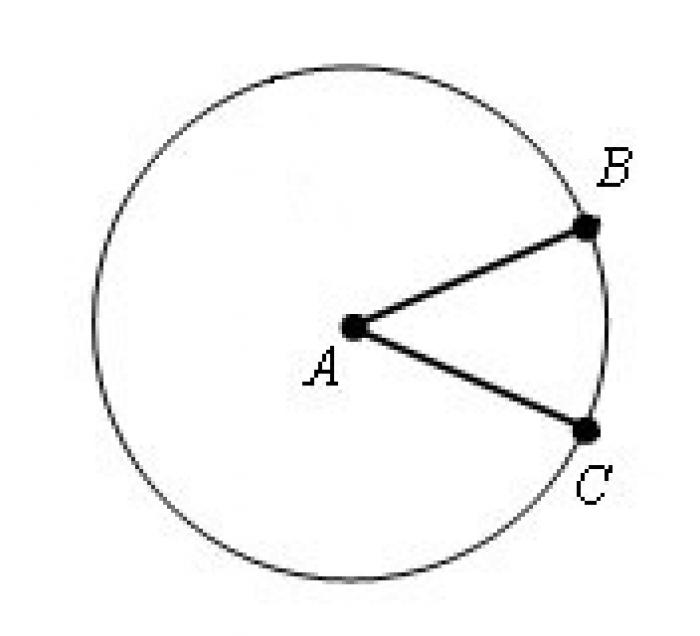
Окружность и ее радиус
Окружность - это замкнутая кривая на плоскости, все точки которой равноудалены от центра. Радиус окружности - это отрезок, соединяющий центр окружности с любой точкой на ней. Длину окружности можно легко вычислить, зная значение радиуса.
Анализ данных
Перед тем, как узнать длину окружности, необходимо проанализировать исходные данные. В задаче может быть дана длина диаметра окружности, который является удвоенной длиной радиуса.
Вычисление длины окружности
Для нахождения длины окружности можно использовать формулу L = 2πR = πD, где L - длина окружности, D - диаметр окружности. Также можно представить диаметр как удвоенный радиус.
Пример
Давайте рассмотрим пример. У нас есть окружность с диаметром 8 см, и мы хотим найти ее длину.
L = 2*3,14*4 = 3,14*8 = 25,12 см
Ответ: длина окружности с диаметром 8 см равна 25,12 см.
Окружность в многоугольниках
Окружность может быть вписана или описана вокруг многоугольника. Если окружность вписана, она будет делить стороны многоугольника пополам. Чтобы найти радиус вписанной окружности, нужно делить площадь многоугольника на половину его периметра.
Окружность в треугольнике и четырехугольнике
Если окружность описана вокруг треугольника, радиус может быть найден по формуле R = a*b*c/4S, где a, b, c - стороны треугольника, S - площадь треугольника. Для описания окружности вокруг четырехугольника, необходимо, чтобы он был выпуклым и чтобы сумма противоположных углов составляла 180°.
Использование трафаретов
Для начертания окружности можно использовать традиционный штангенциркуль или трафареты, которые предлагают окружности разных диаметров. Трафареты можно приобрести в магазинах канцтоваров.