Как найти катет прямоугольного треугольника, если известна гипотенуза

- Треугольник и его составные элементы
- Нахождение катетов прямоугольного треугольника
- Метод 1: использование гипотенузы
- Метод 2: использование известного катета
- Метод 3: использование известного угла
- Метод 4: использование соотношения катетов
- Частные случаи
- Важные замечания
- Полезный совет
Треугольник и его составные элементы
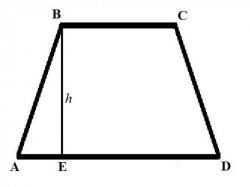
Треугольник – это часть плоскости, ограниченная тремя отрезками прямых, называемых сторонами треугольника, имеющими попарно по одному общему концу, называемых вершинами треугольника. Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным.
Нахождение катетов прямоугольного треугольника
Для нахождения длин катетов прямоугольного треугольника можно использовать различные методы, в зависимости от известных данных.
Метод 1: использование гипотенузы
Если известна длина гипотенузы AC (c), то длину катетов AB (a) и BC (b) можно найти с использованием теоремы Пифагора. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов: a^2 + b^2 = c^2. Из данного уравнения получаем длины катетов: |AB| = a = √ (c^2 - b^2).
Метод 2: использование известного катета
Если известна длина одного из катетов, например |BC| = b, то можно использовать теорему Пифагора для нахождения длины второго катета |AB|. Уравнение будет выглядеть следующим образом: a^2 + b^2 = c^2. Решая это уравнение, получаем длину катета |AB| = a = √ (c^2 - b^2).
Метод 3: использование известного угла
Если известен один из углов прямоугольного треугольника, например ∟α, то можно использовать тригонометрические функции для нахождения длин катетов AB и BC. Синус ∟α равен отношению противолежащего катета к гипотенузе (sin α = b / c), а косинус ∟α равен отношению прилежащего катета к гипотенузе (cos α = a / c). Отсюда можно найти длины катетов: |AB| = a = с * cos α, |BC| = b = c * sin α.
Метод 4: использование соотношения катетов
Если известно соотношение двух катетов, например k = a / b, то можно использовать тригонометрическую функцию котангенс для нахождения длины одного из катетов. В этом случае из уравнения ctg α = a / b мы можем выразить a = b * ctg α. Подставляя это значение в теорему Пифагора a^2 + b^2 = c^2, получаем длину катета b = c / √(ctg^2 α + 1) = c / √(k^2 + 1), где k – заданное соотношение катетов. Аналогично, если известно соотношение катетов b / a, можно использовать тригонометрическую функцию тангенс для нахождения длины катета a.
Частные случаи
Для частных случаев, когда угол ∟α равен 30° или 45°, можно найти длины катетов прямоугольного треугольника без использования уравнений. При ∟α = 30°, длины катетов будут следующими: |AB| = a = c * cos α = c * √3 / 2, |BC| = b = c * sin α = c / 2. При ∟α = 45°, длины всех сторон будут одинаковыми: |AB| = |BC| = a = b = c * √2 / 2.
Важные замечания
При нахождении длин катетов прямоугольного треугольника необходимо учитывать, что длина стороны не может быть отрицательной величиной. Поэтому при извлечении квадратного корня всегда используется положительный знак.
Полезный совет
Для удобства нахождения длин катетов прямоугольного треугольника можно использовать формулы приведения для синуса и косинуса углов. Например, sin β = sin (90° - α) = cos α и cos β = cos (90° - α) = sin α. Это поможет сократить вычисления и упростить задачу.