Как найти косинус, зная синус
- Формула, связывающая синус и косинус угла
- Определение синуса и косинуса угла
- Использование определений для получения формулы
- Теорема Пифагора и уравнение
- Вспомним теорему Пифагора - АВ^2 + BC^2 = AC^2.
- Получение формулы
- Важное замечание
- Величина синуса и косинуса любого угла не может быть больше 1.
Формула, связывающая синус и косинус угла
Для того чтобы получить формулу, связывающую синус и косинус угла, необходимо вспомнить некоторые определения.
Определение синуса и косинуса угла
Синус угла - это отношение противолежащего катета прямоугольного треугольника к гипотенузе. Косинус угла - это отношение прилежащего катета к гипотенузе.
Использование определений для получения формулы
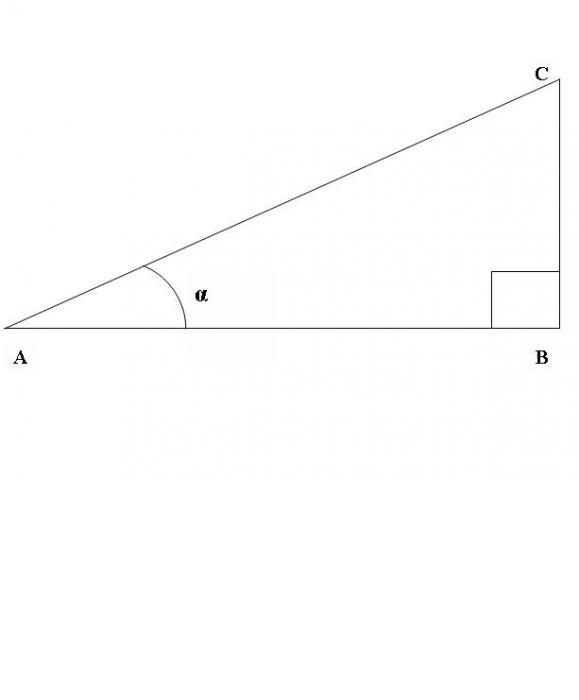
Для получения формулы, связывающей синус и косинус угла, рассмотрим прямоугольный треугольник АВС, где угол АВС - прямой.
Используя определения синуса и косинуса угла, можно записать соотношение sin CAB=BC/AC и cos CAB=AB/AC.
Теорема Пифагора и уравнение
Вспомним теорему Пифагора - АВ^2 + BC^2 = AC^2.
Разделим левую и правую части уравнения на квадрат гипотенузы AC. После этого получим равенство: АВ^2/AC^2 + BC^2/AC^2 = 1.
Получение формулы
Для удобства перепишем равенство, полученное на предыдущем шаге, следующим образом: (AB/AC)^2 + (BC/AC)^2 = 1.
Согласно определениям синуса и косинуса угла, данным на первом шаге, получаем: cos^2(CAB) + sin^2(CAB) = 1.
Из этого можно вывести формулу: cos(CAB) = SQRT(1 - sin^2(CAB)), где SQRT - операция взятия квадратного корня.