Как найти обратную функцию для данной
- Обратная функция и ее особенности
- Получение обратной функции
- Обратная функция для степенных и логарифмических выражений
- Обратная функция для логарифмических функций с основанием 10 или е
- Обратная функция для тригонометрических функций
- Особенности обратной функции
Обратная функция и ее особенности
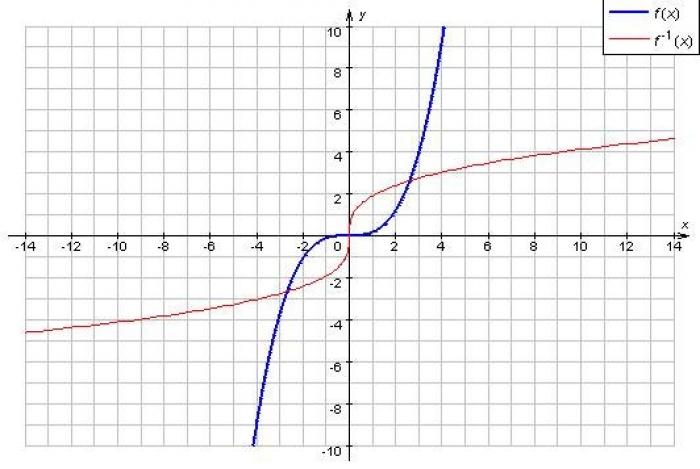
Обратной функцией называется функция, которая меняет роли аргумента и функции в исходной зависимости у = f(x). То есть аргумент x становится функцией от y (x = f(y)). Графики взаимно обратных функций у = f(x) и х = f(y) симметричны относительно оси ординат в первой и третьей координатных четвертях декартовой системы. Областью определения обратной функции является область значений исходной функции, а областью значений - область определения исходной функции.
Получение обратной функции
В общем случае, для нахождения обратной функции у = f(x), можно выразить аргумент x через функцию y, используя правила умножения и переноса многочленов. Например, для простого случая показательной функции у = (7/x) + 11, обращение аргумента x производится элементарно: (7/x) = y - 11, x = 7 * (y - 11). Искомая обратная функция имеет вид x = 7 * (y - 11).
Однако в более сложных функциях, таких как степенные, логарифмические и тригонометрические, необходимо учитывать свойства этих математических выражений при нахождении обратной функции.
Обратная функция для степенных и логарифмических выражений
Если в исходной функции аргумент x находится под степенью, для получения обратной функции нужно взять корень с тем же показателем. Например, для функции у = 7 + x², обратная функция будет иметь вид f(y) = √y - 7.
В случае, когда аргумент x является степенью постоянного числа, применяется определение логарифма. Обратная функция для функции f(x) = аx будет f(y) = logₐy, где основание логарифма а - число, отличное от нуля. И наоборот, для исходной логарифмической функции f(x) = logₐx, обратная функция будет представлять собой степенное выражение: f(y) = аʸ.
Обратная функция для логарифмических функций с основанием 10 или е
В частном случае функции, содержащей натуральный логарифм ln x или десятичный логарифм lg x, обратная функция выражается аналогично, только вместо основания а подставляется экспоненциальное число либо число 10. Например, для функции f(x) = lg x, обратная функция будет f(y) = 10ʸ, а для функции f(x) = ln x, обратная функция будет f(y) = eʸ.
Обратная функция для тригонометрических функций
Обратными друг к другу являются следующие пары тригонометрических функций:
- y = cos x -> x = arccos y;
- y = sin x -> x = arcsin y;
- y = tan x -> x = arctan y.
Особенности обратной функции
Необходимо помнить, что непрерывную функцию можно обратить только на тех промежутках ее значений, где она монотонна. Обратная функция может существовать только на таких промежутках, где исходная функция является строго возрастающей или строго убывающей.






