Как найти период функции
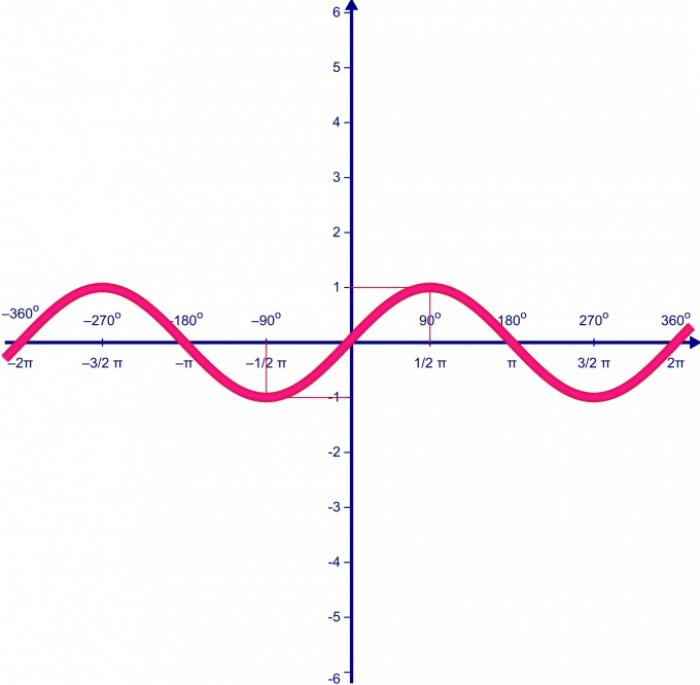
- Периодичность тригонометрических функций
- Как найти период функции
- Пример вычисления периода функции
- Полезный совет
Периодичность тригонометрических функций
Точки на окружности, такие как x, x + 2π, x + 4π и т.д., совпадают друг с другом. Из этого следует, что тригонометрические функции на прямой периодически повторяют свое значение. Если мы знаем период функции, мы можем построить функцию на этом периоде и повторить ее в других местах.
Как найти период функции
Для того чтобы найти период функции, нужно решить уравнение f(x) = f(x+T), где T - период. Мы подставляем значения x и x+T в уравнение и используем уже известные периоды для функций. Для функций синуса и косинуса период составляет 2π, а для тангенса и котангенса - π.
Пример вычисления периода функции
Допустим, у нас есть функция f(x) = sin^2(10x). Мы хотим найти период этой функции.
Рассмотрим выражение sin^2(10x) = sin^2(10(x+T)). Используем формулу понижения степени: sin^2(x) = (1 - cos 2x)/2. Тогда мы получим 1 - cos 20x = 1 - cos 20(x+T), или cos 20x = cos (20x+20T).
Зная, что период косинуса равен 2π, мы можем записать уравнение 20T = 2π. Отсюда получаем, что T = π/10.
Таким образом, T - наименьший положительный период функции. Функция будет повторяться через 2Т, 3Т и в обратном направлении по оси: -T, -2T и так далее.
Полезный совет
Используйте формулы для понижения степени функции. Если вы уже знаете периоды других функций, попробуйте привести данную функцию к известным.






