Как найти степень многочлена
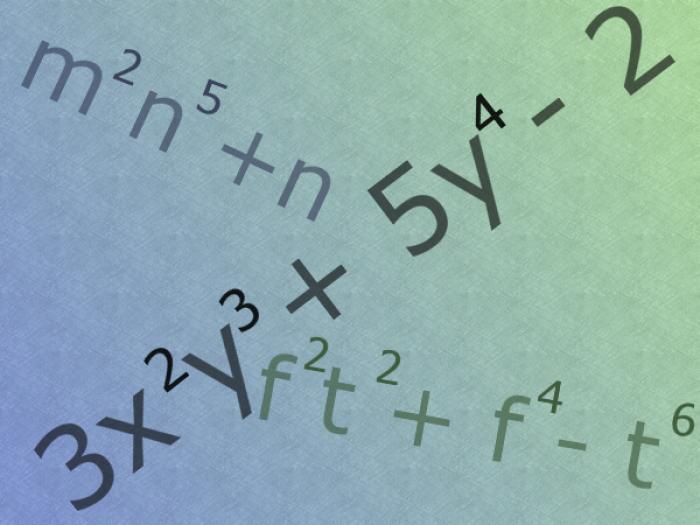
- Понятие многочлена и одночлена
- Определение подобных одночленов
- Шаги по нахождению степени многочлена
- Нахождение степени многочлена по x и y
- Нахождение подобных одночленов
- Соединение подобных одночленов
- Нахождение степени многочлена по x и y
- Вывод по многочлену
- Степень многочлена с корнем
- Нахождение степени многочлена с корнем по y
- Нахождение степени многочлена с корнем по x
- Вывод по многочлену с корнем
- Для многочлена √x+5*y степень по x равна 1/2, а степень по y равна 1.
Понятие многочлена и одночлена
Многочлен - это сумма одночленов. Одночлен же - это произведение нескольких сомножителей, которые являются числом или буквой.
Определение подобных одночленов
Подобные одночлены - это одночлены одинакового вида, то есть одночлены с одинаковыми неизвестными одинаковой степени.
Шаги по нахождению степени многочлена
1. Приведите подобные одночлены, если этого еще не сделано.
2. Примите одну из неизвестных букв за главную. Если она не указана в условии задачи, за главную можно принять любую неизвестную букву.
3. Найдите наивысшую степень для главной буквы. Это максимальная имеющаяся в многочлене степень для этой неизвестной. Именно она и называется степенью многочлена по этой букве.
4. Укажите, если это необходимо, степень многочлена по другим буквам. Таким образом, для многочлена с неизвестными x и y существует степень многочлена по x и степень многочлена по y.
Нахождение степени многочлена по x и y
Возьмите, например, многочлен 2*y²*x³+4*y*x+5*x²+3-y²*x³+6*y²*y²-6*y²*y². В этом многочлене две неизвестных - x и y.
Нахождение подобных одночленов
Найдите подобные одночлены. Здесь есть подобные одночлены члены с y во второй степени и x в третьей. Это 2*y²*x³ и -y²*x³. Еще в данном многочлене есть подобные одночлены с y в четвертой степени. Это 6*y²*y² и -6*y²*y².
Соединение подобных одночленов
Соедините подобные одночлены. Одночлены со второй степенью y и третьей степенью x придут к виду y²*x³, а одночлены с четвертой степенью y сократятся. Получится y²*x³+4*y*x+5*x²+3-y²*x³.
Нахождение степени многочлена по x и y
Примите за главную неизвестную букву x. Найдите максимальную степень при неизвестной x. Это одночлен y²*x³ и, соответственно, степень 3.
Примите за главную неизвестную букву y. Найдите максимальную степень при неизвестной y. Это одночлен y²*x³ и, соответственно, степень 2.
Вывод по многочлену
Степень многочлена 2*y²*x³+4*y*x+5*x²+3-y²*x³+6*y²*y²-6*y²*y² по x равна трем, а по y равна двум.
Степень многочлена с корнем
Учтите, что степень не обязательно является целым числом. Возьмите многочлен √x+5*y. Подобных одночленов у него нет.
Нахождение степени многочлена с корнем по y
Найдите степень многочлена √x+5*y по y. Она равна максимальной степени y, то есть единице.
Нахождение степени многочлена с корнем по x
Найдите степень многочлена √x+5*y по x. Неизвестная x находится под корнем, значит ее степень будет дробью. Так как корень квадратный, то степень x равна 1/2.