Как найти сторону квадратного треугольника
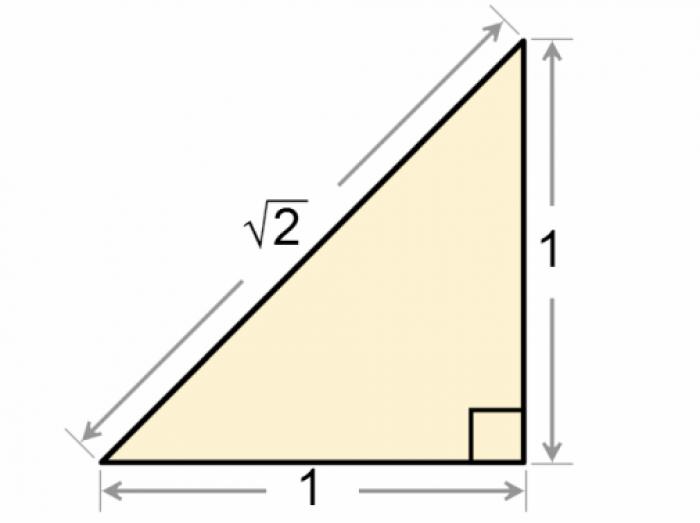
- Как вычислить стороны прямоугольного треугольника?
- 1. Использование теоремы Пифагора
- 2. Вычисление гипотенузы
- 3. Вычисление катета
- 4. Использование таблиц Брадиса
- 5. Вычисление катетов с помощью тригонометрических функций
- 6. Вычисление углов прямоугольного треугольника
- 7. Вычисление гипотенузы и катета
Как вычислить стороны прямоугольного треугольника?
Прямоугольный треугольник, также известный как квадратный треугольник, имеет особые соотношения между сторонами и углами. Для вычисления сторон этой геометрической фигуры вам потребуется некоторые инструменты, такие как лист бумаги, ручка, таблицы Брадиса и калькулятор. В этой статье мы рассмотрим несколько способов решения задач по вычислению сторон прямоугольного треугольника.
1. Использование теоремы Пифагора
Теорема Пифагора гласит, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Для применения этой теоремы необходимо знать длину как минимум двух сторон треугольника. Вы можете вычислить длину гипотенузы, если известны размеры катетов треугольника, или вычислить длину одного из катетов, если известны размеры гипотенузы и другого катета.
2. Вычисление гипотенузы
Если известны размеры катетов, вы можете вычислить длину гипотенузы с помощью калькулятора. Возведите каждый катет в квадрат, сложите полученные значения и извлеките квадратный корень из суммы. Так вы найдете длину гипотенузы.
3. Вычисление катета
Если известны размеры гипотенузы и одного из катетов, вы можете вычислить длину другого катета с помощью калькулятора. Извлеките квадратный корень из разности квадрата гипотенузы и квадрата известного катета. Таким образом, вы найдете длину второго катета.
4. Использование таблиц Брадиса
Если заданы гипотенуза и один из прилежащих острых углов, вы можете использовать таблицы Брадиса. В них содержатся значения тригонометрических функций для различных углов. С помощью калькулятора и функций синуса и косинуса, а также тригонометрических теорем, вы можете вычислить значения сторон прямоугольного треугольника.
5. Вычисление катетов с помощью тригонометрических функций
Основные тригонометрические функции могут быть использованы для вычисления катетов прямоугольного треугольника. Если известны гипотенуза и один из острых углов, можно вычислить длину противолежащего катета с помощью функции синуса, а длину прилежащего катета - с помощью функции косинуса. Аналогично, если известны гипотенуза и другой острый угол, можно использовать функции синуса и косинуса для нахождения размеров катетов.
6. Вычисление углов прямоугольного треугольника
Если известен катет и прилежащий к нему острый угол, можно вычислить противолежащий угол с помощью формулы α = 90° – β или с использованием тригонометрических формул приведения. Это может быть полезно, когда вам нужно найти значение угла в прямоугольном треугольнике.
7. Вычисление гипотенузы и катета
Если известен катет и противолежащий ему острый угол, можно вычислить гипотенузу с помощью тригонометрических функций и таблиц Брадиса. Также можно вычислить значение прилежащего катета с помощью функции тангенса.
Используя описанные методы и инструменты, вы сможете легко вычислить стороны прямоугольного треугольника. Это будет полезно при решении задач и заданий в области геометрии и тригонометрии.






