Как найти уравнение биссектрисы
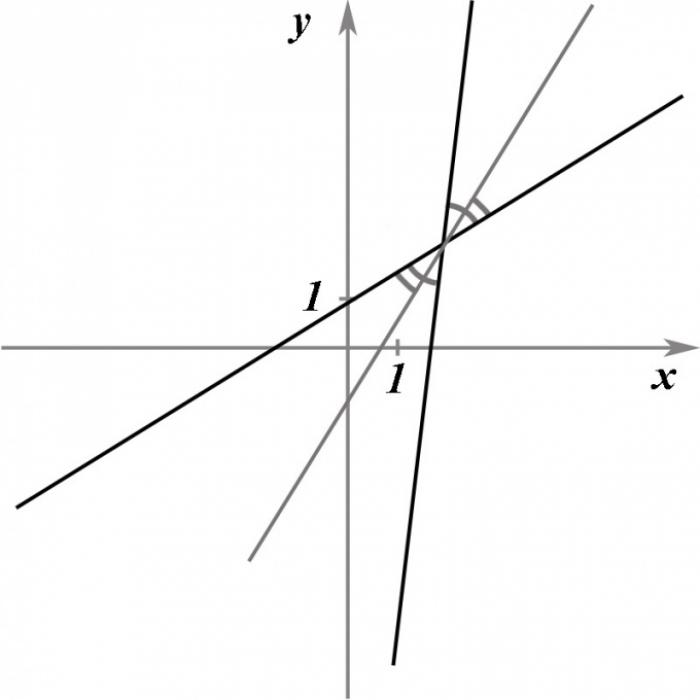
Нахождение уравнения биссектрисы угла между двумя пересекающимися прямыми
Инструкция 1
Предположим, что у нас есть две пересекающиеся прямые, заданные своими каноническими уравнениями A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0. Важно, чтобы A1/B1 ≠ A2/B2, иначе прямые будут параллельны и задача будет не иметь смысла.
Инструкция 2
Так как две пересекающиеся прямые образуют четыре равных угла между собой, существуют ровно две прямые, которые делят пополам угол между ними и являются биссектрисами.
Инструкция 3
Эти две прямые будут перпендикулярны друг другу. Это можно легко доказать, так как сумма четырех углов, образованных пересекающимися прямыми, всегда равна 360°. Поскольку углы попарно равны, то сумма углов a и b будет равна 180°. Угол между биссектрисами всегда равен a/2 + b/2 = (a + b)/2 = 90°.
Инструкция 4
Биссектриса делит угол между прямыми пополам, значит для любой точки, лежащей на ней, расстояния до обеих прямых будут одинаковыми.
Инструкция 5
Если прямая задана каноническим уравнением, то расстояние от нее до некоторой точки (x0, y0), не лежащей на этой прямой, можно выразить следующей формулой: d = |(Ax0 + By0 + C)/(√(A^2 + B^2))|. Для точки, лежащей на биссектрисе, это расстояние должно быть одинаковым для обеих прямых.
Инструкция 6
Из-за того, что в обеих частях равенства стоят знаки модуля, оно описывает сразу обе искомые прямые. Чтобы превратить его в уравнение только одной из биссектрис, нужно раскрыть модуль либо со знаком +, либо со знаком -. Таким образом, уравнение первой биссектрисы будет выглядеть как (A1*x + B1*y + C1)/√(A1^2 + B1^2) = (A2*x + B2*y + C2)/√(A2^2 + B2^2), а уравнение второй биссектрисы: (A1*x + B1*y + C1)/√(A1^2 + B1^2) = -(A2*x + B2*y + C2)/√(A2^2 + B2^2).
Пример
Допустим, у нас есть прямые, заданные каноническими уравнениями: 2x + y -1 = 0 и x + 4y = 0. Уравнение первой биссектрисы получается из равенства: (2x + y -1)/√5 = (x + 4y)/√15. Раскрывая скобки и переводя уравнение в канонический вид, получаем (2*√3 - 1)*x + (√3 - 4)*y - √3 = 0.
Таким образом, нахождение уравнения биссектрисы угла между двумя пересекающимися прямыми возможно с использованием указанных выше инструкций и формул. Этот метод помогает найти уравнение прямой, которая делит пополам угол между двумя пересекающимися прямыми.