Как определить центр тяжести тела
- Определение центра тяжести геометрических предметов
- Неоднородные предметы и их центр тяжести
- Простые формы и центр тяжести
- Линейка и карандаш для определения центра тяжести
- Центр тяжести сложных форм
Определение центра тяжести геометрических предметов
Центр тяжести является важной характеристикой для любого геометрического предмета. Он представляет собой точку пересечения всех сил тяжести, действующих на фигуру при изменении ее положения. Иногда центр тяжести может находиться вне границ тела.
Неоднородные предметы и их центр тяжести
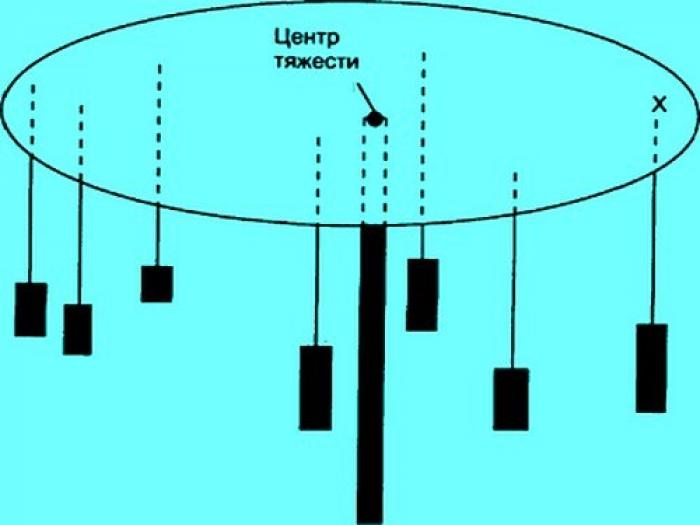
Рассчитать центр тяжести для неоднородного предмета произвольной формы может оказаться непростой задачей. Однако, существует способ, позволяющий найти эту точку опытным путем. Для этого можно воспользоваться свободным подвешиванием тела на нити и найти точку пересечения всех сил тяжести при его переворачивании.
Простые формы и центр тяжести
У простых форм, таких как прямоугольник, круг, шар или цилиндр, центр тяжести совпадает с центром симметрии. Например, у однородного круглого диска он находится в точке пересечения диаметров. У обруча и шара центр тяжести также находится в геометрическом центре, но вне пределов фигуры. Для определения центра тяжести прямоугольного параллелепипеда нужно найти точку пересечения его диагоналей.
Линейка и карандаш для определения центра тяжести
Для определения центра тяжести сложных форм тел можно воспользоваться линейкой и карандашом. Необходимо начертить вертикальные линии, совпадающие с направлением нитей, закрепленных в различных точках предмета. В зависимости от сложности формы, проведите две или три линии, которые должны пересекаться в одной точке. Именно эта точка будет являться центром тяжести выбранного предмета.
Центр тяжести сложных форм
Способ подвешивания предмета позволяет определить центр тяжести как для плоских фигур, так и для более сложных тел с непостоянной произвольной формой. Например, для разложенного состояния двух брусков, соединенных шарниром, центр тяжести находится в их геометрическом центре. Однако, если бруски согнуть, то центр тяжести окажется за пределами предметов.
Центр тяжести является важной характеристикой для анализа и понимания поведения геометрических предметов. Определение этого параметра позволяет предсказать, как предмет будет двигаться и взаимодействовать с другими объектами. Рассмотренные выше методы позволяют определить центр тяжести для разных форм и типов предметов, что делает их полезными инструментами для изучения и практического применения геометрии.