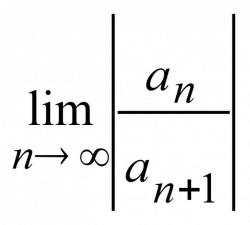Как найти векторное произведение векторов
- Векторное произведение векторов: ключевое понятие в векторном анализе
- Правила векторного произведения в трехмерном пространстве
- Векторное произведение параллельных и перпендикулярных векторов
- Определение направления вектора с
- Векторное произведение и скалярное произведение
- Важность порядка следования векторов в квадратных скобках
Векторное произведение векторов: ключевое понятие в векторном анализе
Векторное произведение является одним из ключевых понятий векторного анализа. В физике различные величины находятся путем векторного произведения двух других величин. Осуществлять векторные произведения и преобразования на его основе нужно очень аккуратно, соблюдая основные правила.
Правила векторного произведения в трехмерном пространстве
Векторное произведение вектора a на вектор b в трехмерном пространстве записывается в виде c = [ab]. При этом вектор с должен удовлетворять ряду требований. Длина вектора с равна произведению длин векторов a и b на синус угла между ними: |с| = |a||b|*sin(a^b). Вектор с ортогонален вектору a и ортогонален вектору b. Тройка векторов abc является правой.
Векторное произведение параллельных и перпендикулярных векторов
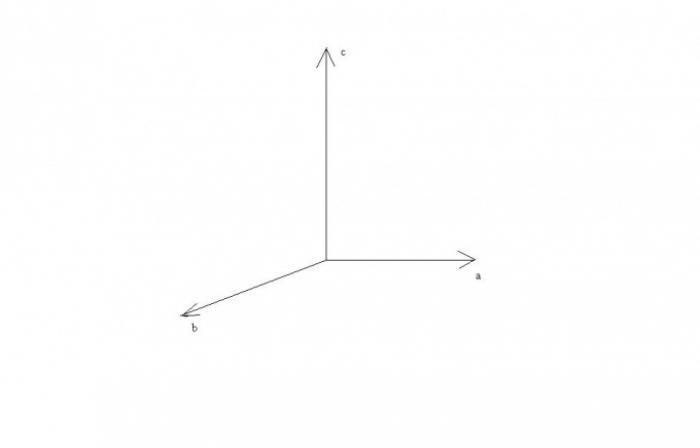
Из этих правил видно, что если векторы a и b параллельны или лежат на одной прямой, то их векторное произведение равно нулевому вектору, так как синус угла между ними равен нулю. В случае перпендикулярности векторов a и b, векторы a, b и c будут перпендикулярны друг другу и их можно представить лежащими на осях прямоугольной декартовой системы координат.
Определение направления вектора с
Исходя из того, что тройка векторов abc является правой, направление вектора c можно найти по правилу правой руки. Сожмите руку в кулак, а затем направьте указательный палец вперед по направлению вектора a. Средний палец направьте по направлению вектора b. Тогда большой палец, направленный вверх, перпендикулярно указательному и среднему пальцу будет указывать направление вектора с.
Векторное произведение и скалярное произведение
Нельзя путать векторное произведение со скалярным! В результате векторного произведения получается вектор, в результате скалярного - скаляр, как следует из названия.
Важность порядка следования векторов в квадратных скобках
Векторное произведение является антикоммутативным, то есть [ab] = -[ba]. То есть порядок следования векторов в квадратных скобках очень важен!
Вывод: векторное произведение является важным понятием в векторном анализе, позволяющим находить различные величины в физике. Оно имеет свои правила, включая определение направления и длины вектора, а также требование правой тройки векторов. При использовании векторного произведения необходимо отличать его от скалярного произведения и помнить о важности порядка следования векторов.