Как определить функцию по графику
- Координатные плоскости и графики функций
- Прямая линия как график функции
- Направление и уравнение функции
- Парабола и ее вид
- Кубическая парабола и квадратичная функция
- Гипербола и ее форма
Координатные плоскости и графики функций
Координата абсолютно любой точки на плоскости определяется двумя ее величинами: по оси абсцисс и оси ординат. Совокупность множества таких точек и представляет собой график функции. По нему вы видите, как меняется значение Y в зависимости от изменения значения Х. Также вы можете определить, на каком участке (промежутке) функция возрастает, а на каком убывает.
Прямая линия как график функции
Что можно сказать о функции, если ее график представляет собой прямую линию? Посмотрите, проходит ли эта прямая через точку начала отсчета координат (то есть, ту, где величины Х и Y равны 0). Если проходит, то такая функция описывается уравнением y = kx. Легко понять, что чем больше будет значение k, тем ближе к оси ординат будет располагаться эта прямая. А сама ось Y фактически соответствует бесконечно большому значению k.
Направление и уравнение функции
Посмотрите на направление функции. Если она идет «слева снизу – направо наверх», то есть через 3-ю и 1-ю координатные четверти, она возрастающая, если же «слева сверху – направо вниз» (через 2-ю и 4-ю четверти), то она убывающая.
Когда прямая не проходит через начало координат, она описывается уравнением y = kx + b. Прямая пересекает ось ординат в точке, где y = b, и значение y может быть как положительным, так и отрицательным.
Парабола и ее вид
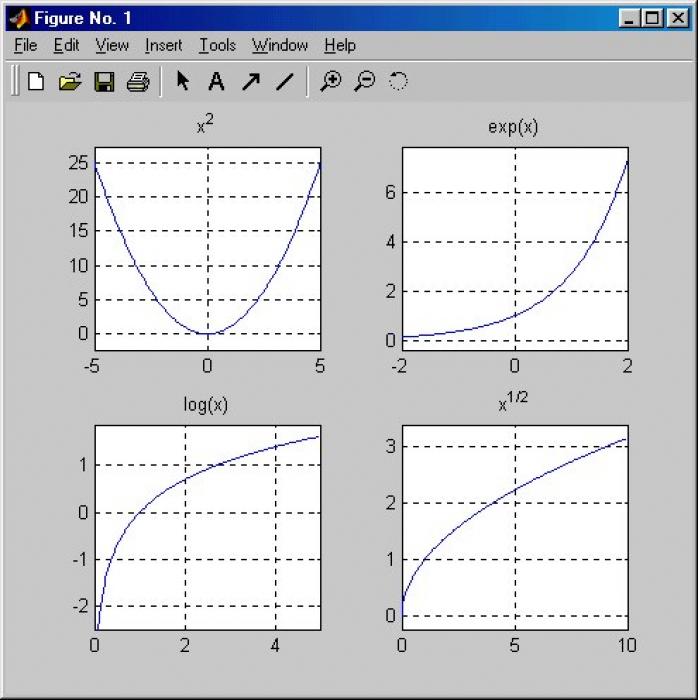
Функция называется параболой, если описывается уравнением y = x^n, и ее вид зависит от величины n. Если n – любое четное число (простейший случай – квадратичная функция y = x^2), график функции представляет собой кривую, проходящую через точку начала координат, а также через точки с координатами (1;1), (-1;1), поскольку единица в любой степени останется единицей. Все значения y, соответствующие любым значениям X, отличным от нуля, могут быть только положительными. Функция симметрична относительно оси Y, а ее график расположен в 1-й и 2-й координатных четвертях. Легко можно понять, что чем больше величина n, тем приближеннее график будет к оси Y.
Кубическая парабола и квадратичная функция
Если n – нечетное число, график этой функции представляет собой кубическую параболу. Кривая располагается в 1-й и 3-й координатных четвертях, симметрична относительно оси Y и проходит через начало координат, а также через точки (-1;-1), (1;1). Когда квадратичная функция представляет собой уравнение y = ax^2 + bx + c, форма параболы совпадает с формой в простейшем случае (y = x^2), однако ее вершина не находится в точке начала координат.
Гипербола и ее форма
Функция называется гиперболой, если она описывается уравнением y = k/x. Легко можно видеть, что при значении х, стремящемся к 0, значение y возрастает до бесконечности. График функции представляет собой кривую, состоящую из двух ветвей и располагающуюся в разных координатных четвертях.