Как построить однополосный гиперболоид
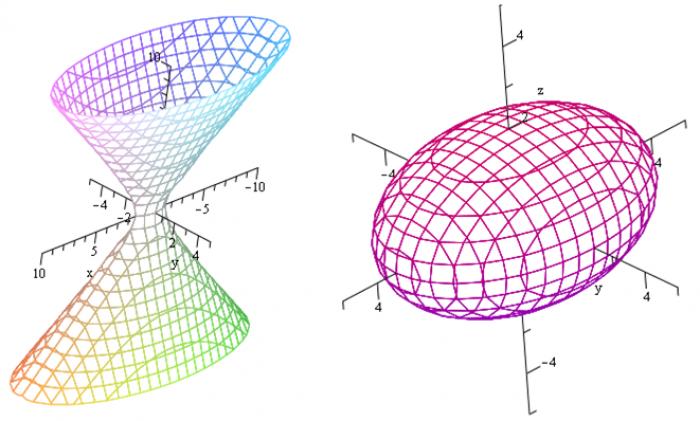
- Как построить однополосный гиперболоид
- Шаг 1: Построение гиперболы в плоскости Xoz
- Шаг 2: Построение гиперболы в плоскости Oyz
- Шаг 3: Построение параллелограмма в плоскости Oxy
- Шаг 4: Построение остальных эллипсов
- Описание однополосного гиперболоида
- Дополнительная информация
Как построить однополосный гиперболоид
Однополосный гиперболоид - это пространственная фигура, которая может быть построена с помощью определенной методики. Для этого вам понадобятся карандаш, бумага и математический справочник.
Шаг 1: Построение гиперболы в плоскости Xoz
Для начала, нарисуйте две полуоси, которые совпадают с осью y (действительная полуось) и с осью z (мнимая полуось). Затем, используя эти полуоси, постройте гиперболу.
Далее, задайте определенную высоту h для гиперболоида. Продолжите проводить прямые, параллельные оси Ox, на уровне этой заданной высоты. Эти прямые должны пересекать график гиперболы в двух точках: нижней и верхней.
Шаг 2: Построение гиперболы в плоскости Oyz
Повторите вышеописанные действия в другой плоскости, на этот раз в плоскости Oyz. Здесь вы должны построить гиперболу, в которой действительная полуось проходит через ось y, а мнимая полуось совпадает с осью z.
Шаг 3: Построение параллелограмма в плоскости Oxy
Теперь постройте параллелограмм в плоскости Oxy, соединив точки графиков гипербол. Затем вычертите горловой эллипс таким образом, чтобы он вписался в построенный ранее параллелограмм.
Шаг 4: Построение остальных эллипсов
Повторите описанные выше действия для построения остальных эллипсов. В результате вы получите чертеж однополосного гиперболоида.
Описание однополосного гиперболоида
Однополосный гиперболоид описывается уравнением, где a и b являются действительными полуосями, а c - мнимой полуосью. Координатные плоскости гиперболоида также являются плоскостями симметрии, а начало координат - его центром симметрии.
Дополнительная информация
Если две полуоси однополосного гиперболоида равны, то фигуру можно получить путем вращения гиперболы вокруг мнимой оси. Также, при рассмотрении этой фигуры относительно осей Oxz и Oyz видно, что главными сечениями являются гиперболы, а сечение плоскостью Oxy представляет собой эллипс. Горловой эллипс однополосного гиперболоида проходит через начало координат, так как z=0. Уравнение горлового эллипса: x²/a² +y²/b²=1, а другие эллипсы составляются по уравнению x²/a² +y²/b²=1+h²/c².