Как построить сечение куба
- Построение сечения куба
- Разбор общей задачи построения сечения куба
- Решение задачи
- Построение первой стороны сечения
- Построение второй стороны сечения
- Построение третьей стороны сечения
- Построение четвертой стороны сечения
Построение сечения куба
Сечение любой объемной геометрической фигуры должно быть задано несколькими параметрами, чтобы оно однозначно могло быть найдено. В данной задаче построения сечения куба, секущая плоскость задается прямой пересечения ее собственной плоскости с плоскостью, содержащей нижнее основание куба и углом наклона к этой плоскости. Для выполнения задачи вам понадобятся несколько инструментов, таких как бумага, ручка, линейка и циркуль.
Разбор общей задачи построения сечения куба
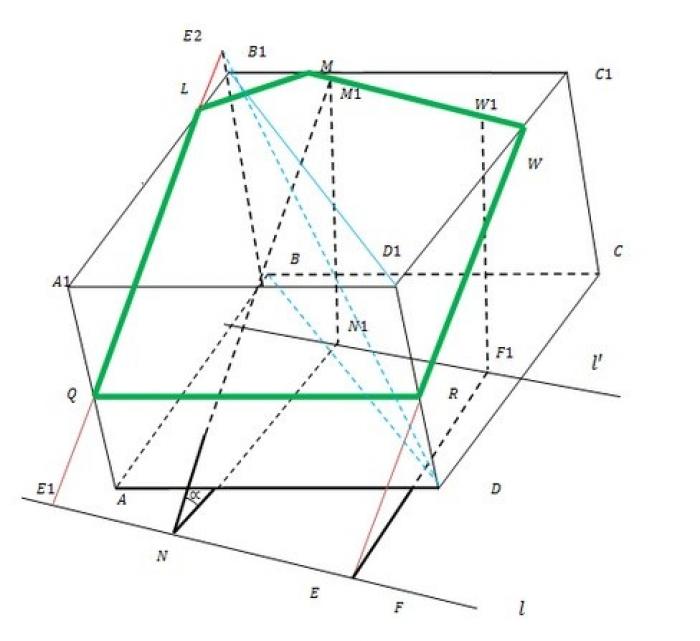
Прежде чем приступить к самому построению, необходимо подробнее разобрать общую задачу построения сечения куба. Секущая плоскость задана прямой пересечения ее собственной плоскости с плоскостью, содержащей нижнее основание параллелепипеда и углом наклона к этой плоскости. Данный принцип построения иллюстрирован на рисунке.
Решение задачи
В геометрических задачах на построение, любой угол задается не самим углом, а какой-либо его тригонометрической функцией. В данной задаче используется котангенс (ctg). Необходимо отмерить длину Нctgф = d с помощью циркуля и перевести эту величину в масштаб задачи.
Построение первой стороны сечения
На прямой l, которая является прямой пересечения секущей плоскости с плоскостью, содержащей нижнее основание куба, выберите две произвольные точки N и F. Из этих точек проведите дуги радиуса d внутри нижнего основания куба. К этим дугам проведите общую касательную до ее пересечения с ребрами АВ и СD. Обозначьте точки касания как N1 и F1.
Построение второй стороны сечения
Из точек N1 и F1 проведите перпендикуляры M1 и W1 на верхнее основание куба, длина которых равна Н. Продлите отрезок M1W1 до его пересечения с ребрами В1С1 и С1D1 куба. Таким образом, вы найдете первую сторону искомого сечения MW.
Построение третьей стороны сечения
В пределах плоскости, содержащей боковую грань DCC1D1, проведите прямую WE из точки W (Е - ее пересечение с прямой l). Пересечение WE с ребром D1D даст точку R. Отрезок WR будет вторым ребром искомого сечения.
Построение четвертой стороны сечения
Продлите боковое ребро куба ВВ1 в направлении от В до В1. В плоскости диагонального сечения куба BB1D1D, из точки R проведите прямую до ее пересечения с продлением ВВ1 в точке Е2. Из точки Е2 опустите прямую до ее пересечения с прямой l в точке Е1. Прямая Е1Е2 пересекает боковые ребра куба А1В1 и АА1 в точках L и Q соответственно. Таким образом, ML, LQ и QR являются оставшимися искомыми ребрами сечения куба.
Теперь, следуя описанным шагам и используя необходимые инструменты, вы сможете построить сечение куба.