Как строить эллипс
- Построение эллипса
- Построение эллипса с помощью нити и булавок
- Описание геометрических характеристик эллипса
- Построение эллипса вписыванием в окружность
- Построение эллипса по двум окружностям
Построение эллипса
Предметы, имеющие эллиптическую форму, окружают нас повсюду. В частности, именно такую форму имеет Земля и другие планеты Солнечной системы. Данная геометрическая фигура занимает особое место в аналитической геометрии, а сечение эллипса является главной составляющей тел вращения.
Построение эллипса с помощью нити и булавок
Эллипсом называется кривая, состоящая из всех точек плоскости, отвечающих следующему критерию: сумма расстояний от двух точек этой плоскости является постоянной величиной. Существуют три способа построения этой кривой с помощью нити, вписыванием в окружность и по двум окружностям.
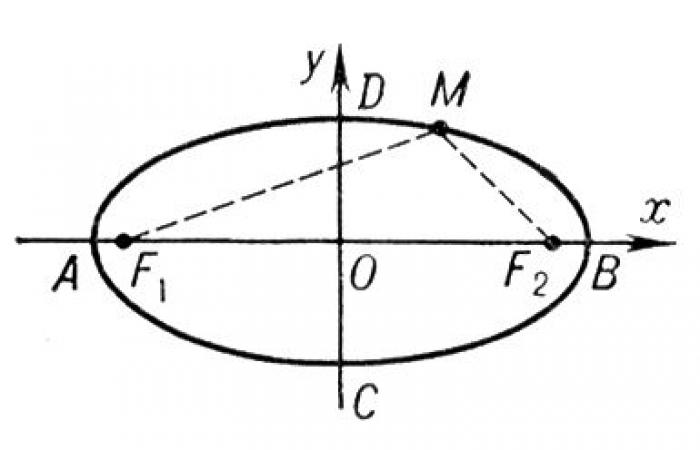
Для построения эллипса первым способом вам потребуются две булавки, которые необходимо прикрепить к бумаге, образовав тем самым две неподвижные точки F1 и F2, а также карандаш, при помощи которого будет строиться эллипс. Расположив булавки указанным образом, чуть выше отметьте точку М, таким образом, чтобы было справедливо соотношение MF1 > MF2. Натягивая нить и передвигая карандаш, опишите вытянутую линию, которая и будет эллипсом. Расстояние между точками F1 и F2 называется фокусным расстоянием, а сами эти точки - фокусами.
Описание геометрических характеристик эллипса
Если отрезок с фокусным расстоянием прочертить до его пересечения с эллипсом, получится большая ось эллипса - AB. Соответственно, если через центр эллипса O провести прямую, перпендикулярную AB и имеющую оба конца на линии эллипса, то получится малая ось эллипса, называемая DC. Все это показано на рисунке 1. Каноническое уравнение эллипса выглядит следующим образом: x^2/a^2 + y^2/b^2 = 1, где a = AO = OB, b = DO = OC.
Построение эллипса вписыванием в окружность
Второй способ построения эллипса основывается на вписывании его в окружность. Для этого на большой оси эллипса постройте окружность. Большая ось эллипса A1A2 будет являться для окружности диаметром. Из точки окружности, заданной произвольно, проведите перпендикуляр к большой оси эллипса. Его длину поделите на некоторую, заранее заданную величину, после чего отметьте на перпендикуляре отрезок, длина которого равна результату деления - его конец и будет одной из точек эллипса. Затем постройте другую прямую, параллельную предыдущей, и проделайте с ней то же самое. Чем больше раз вы повторите эту операцию, тем точнее будет построен эллипс. Так можно построить бесконечное число эллипсов, вписанных в окружность.
Построение эллипса по двум окружностям
Согласно третьему способу, эллипс строится по двум окружностям. Для этого прочертите сначала первую окружность, диаметр которой равен большой оси эллипса, а затем вторую, диаметр которой равен предполагаемому фокусному расстоянию эллипса. Большую окружность разделите на несколько частей прямыми, проведенными через центр окружности. Затем проведите через большую окружность прямые, параллельные CD, а через меньшую - параллельные AB, таким образом, чтобы эти прямые между собой пересекались, как показано на рисунке 2. Точки пересечения этих прямых и будут точками эллипса. Соединив их между собой, вы получите эллипс.
Теперь вы знаете несколько способов построения эллипса и можете использовать их в своих проектах или задачах. Эллипсы имеют множество применений в геометрии, физике и других науках, поэтому знание и умение строить их может быть полезным инструментом.






