Как вписать равносторонний треугольник в окружность
- Вписывание равностороннего треугольника в построенную окружность
- Шаг 1: Построение хорды
- Шаг 2: Построение перпендикуляра
- Шаг 3: Построение второго перпендикуляра
- Шаг 4: Определение радиуса окружности
- Шаг 5: Нахождение точек равностороннего треугольника
- Шаг 6: Вписывание равностороннего треугольника
Вписывание равностороннего треугольника в построенную окружность
Задачи на геометрические построения являются важной частью школьной программы обучения, поскольку развивают пространственное и логическое мышление учащихся. В рамках этих задач существуют типовые и нетиповые варианты. К одной из типовых задач можно отнести вписывание равностороннего треугольника в окружность. Однако, вопрос возникает: как выполнить данное построение, если окружность уже построена?
Шаг 1: Построение хорды
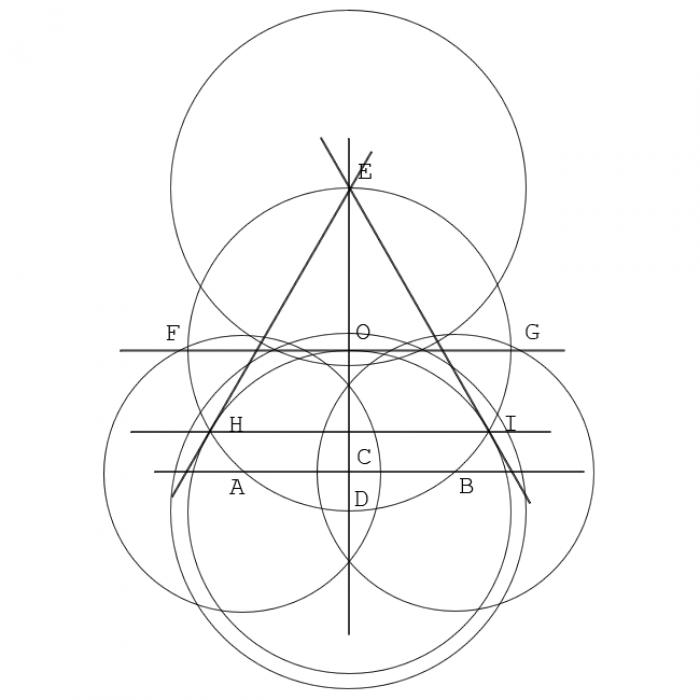
Для начала необходимо построить хорду на уже заданной окружности. С помощью линейки проведите отрезок так, чтобы он пересекал окружность в двух точках. Назовем эти точки A и B. Чтобы обеспечить оптимальное расположение точек, рекомендуется выбирать точки A и B на достаточном удалении друг от друга.
Шаг 2: Построение перпендикуляра
Постройте перпендикуляр, пересекающий отрезок AB и делящий его точкой пересечения на две равные части. Установите расстояние между ножками циркуля, которое немного меньше длины отрезка AB, но больше половины его длины. Установите иглу циркуля в точку A и постройте окружность. Затем установите иглу циркуля в точку B и постройте еще одну окружность. Проведите отрезок через точки пересечения вычерченных окружностей так, чтобы он пересекал отрезок AB в одной точке (назовем ее точкой C), а первоначальную окружность - в двух точках (назовем их точками D и E).
Шаг 3: Построение второго перпендикуляра
Постройте перпендикуляр, пересекающий отрезок DE и делящий его точкой пересечения на две равные части, используя аналогичный метод, описанный во втором шаге. Пусть построенный отрезок пересекает окружность в точках F и G, а отрезок DE - в точке O. Точка O будет центром окружности.
Шаг 4: Определение радиуса окружности
Установите расстояние между ножками циркуля, равное радиусу окружности. Поместите иглу циркуля в точку D и поместите конец другой ножки циркуля в точку O.
Шаг 5: Нахождение точек равностороннего треугольника
Найдите точки двух углов равностороннего треугольника, вписанного в окружность. Не изменяя положения ножки циркуля с иглой (в точке D) и расстояния между ножками циркуля, установленного на предыдущем шаге, начертите окружность. Эта окружность пересечет первоначальную окружность в двух точках. Пусть эти точки будут обозначены H и I.
Шаг 6: Вписывание равностороннего треугольника
Чтобы вписать равносторонний треугольник в окружность, соедините отрезками точки E, H и I. Треугольник со сторонами EH, HI и EI будет равносторонним и вписанным в исходную окружность.
Геометрические построения не только развивают логическое мышление, но и помогают ученикам лучше понять и визуализировать геометрические концепции. Построение равностороннего треугольника в окружности - одна из таких задач, которая требует применения знаний о прямых и окружностях, а также использования инструментов, таких как линейка, карандаш и циркуль.