Как вычесть дробь с разными знаменателями
- Числа и их запись
- Запись чисел
- Ограниченная точность десятичных дробей
- Дроби в арифметических операциях
- Вычитание дробей
Числа и их запись
Одной из важных особенностей человеческого разума является его способность к абстрактному мышлению. В этом контексте числа играют особую роль, представляя собой одну из наивысших форм абстракции в нашем мире. Существует несколько категорий чисел, каждая из которых имеет свои уникальные свойства. Однако, самыми распространенными и часто используемыми в повседневной жизни являются целые и действительные числа.
Запись чисел
В нашей культуре числа обычно записываются в десятичной системе счисления. Это означает, что каждая цифра числа имеет свое место в числовом ряду, которое определяется ее позицией относительно точки. Для действительных чисел, которые включают в себя и целые числа, и десятичные дроби, используется запись в виде десятичных чисел.
Ограниченная точность десятичных дробей
Недостатком записи дробных чисел в виде десятичных дробей является их ограниченная точность. В некоторых случаях это не имеет большого значения, но когда точность играет важную роль, нам необходимо использовать другой способ записи чисел.
Дроби в арифметических операциях
Вместо десятичной записи, числа могут быть записаны в виде дробей, состоящих из числителя и знаменателя. Это позволяет нам работать с числами, сохраняя их точность. Однако, арифметические операции с дробями могут быть более сложными, чем с десятичными числами. Например, для вычитания дробей с разными знаменателями необходимо выполнить несколько математических действий.
Вычитание дробей
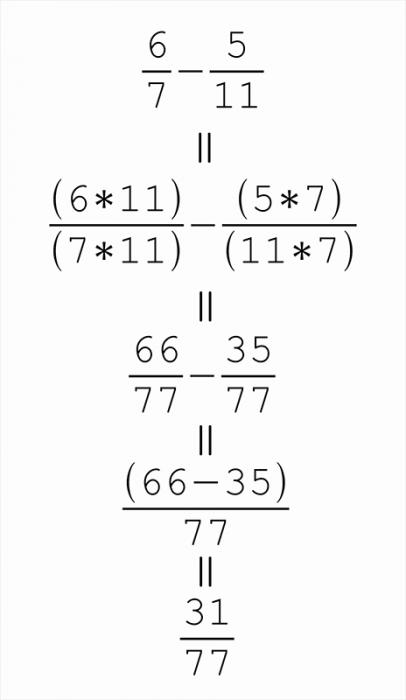
Если вам необходимо вычесть одну дробь из другой, вам потребуется калькулятор или лист бумаги с ручкой. Следуйте следующим инструкциям:
1. Приведите дроби к общему знаменателю. Умножьте числитель и знаменатель первой дробробей. Вычтите из числителя первой дроби числитель второй дроби. Запишите полученное значение в качестве числителя результирующей дроби, а общий знаменатель оставьте без изменений.
3. Если необходимо, сократите дробь-результат. Подберите наибольший общий делитель для числителя и знаменателя результирующей дроби. Делите числитель и знаменатель на этот делитель и запишите новые значения в качестве числителя и знаменателя итоговой дроби.
В некоторых случаях наибольший общий делитель может не существовать. В таком случае оставьте исходную дробь в качестве результата.
Теперь, когда вы знаете, как вычитать дроби с разными знаменателями, вы сможете легче выполнять подобные арифметические операции.