Как вычислить объем конуса
- Вычисление объема конуса
- Способы задания конуса
- Вычисление объема конуса по радиусу и высоте
- Вычисление объема конуса по радиусу основания и длине боковой стороны
- Вычисление объема конуса по углу при вершине и высоте
- Вычисление радиуса основания по углу при вершине и высоте
Вычисление объема конуса
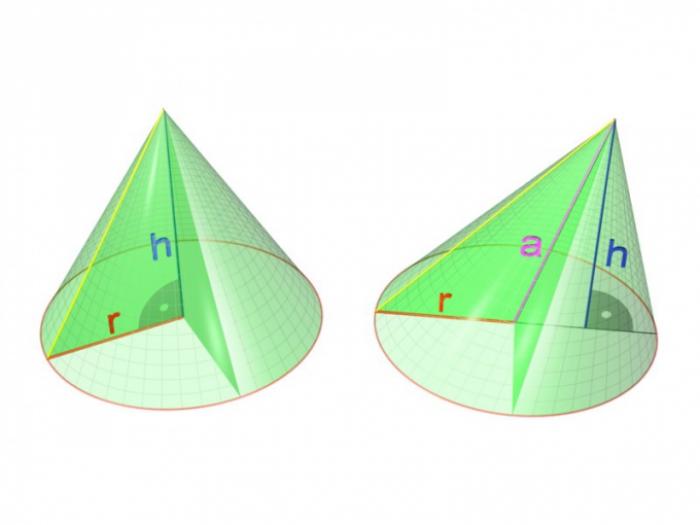
Конус (точнее, круговой конус) — тело, образованное вращением прямоугольного треугольника вокруг одного из его катетов. Будучи трехмерным телом, конус характеризуется, кроме всего прочего, объемом. Этот объем нужно уметь вычислять.
Способы задания конуса
Конус можно задать разными способами. Например, может быть известен радиус его основания и длина боковой стороны. Другой вариант — радиус основания и высота. Наконец, еще один способ задания кругового конуса состоит в том, чтобы указать угол при его вершине и высоту. Как легко убедиться, все эти способы определяют круговой конус однозначно.
Вычисление объема конуса по радиусу и высоте
Чаще всего известны радиус основания и высота конуса. В этом случае вначале нужно вычислить площадь основания. По формуле круга она будет равна πR^2, где R — радиус основания конуса. Тогда объем всего тела равняется πR^2*h/3, где h — высота конуса. Эту формулу легко проверить с помощью интегрального исчисления. Таким образом, объем кругового конуса ровно втрое меньше объема цилиндра с теми же самыми основанием и высотой.
Вычисление объема конуса по радиусу основания и длине боковой стороны
Если высота не задана, а вместо этого известны радиус основания и длина боковой стороны, то для определения объема вначале придется найти высоту. Поскольку боковая сторона представляет собой гипотенузу прямоугольного треугольника, а радиус основания служит одним из его катетов, то высота будет вторым катетом того же самого треугольника. По теореме Пифагора h = √(l^2 - R^2), где l — длина боковой стороны конуса. Очевидно, что эта формула будет иметь смысл только тогда, когда l ≥ R. При этом, если l = R, то высота обращается в ноль, поскольку конус в этом случае превращается в круг. Если же l < R, то существование такого конуса невозможно.
Вычисление объема конуса по углу при вершине и высоте
Если известен угол при вершине конуса и его высота, то для вычисления объема потребуется найти радиус основания. Чтобы это сделать, придется обратиться к геометрическому определению конуса как тела, образованного вращением прямоугольного треугольника. При этом известный угол при вершине будет вдвое больше соответствующего угла этого треугольника. Поэтому угол при вершине удобно обозначить 2α. Тогда угол треугольника будет равен α.
Вычисление радиуса основания по углу при вершине и высоте
По определению тригонометрических функций, искомый радиус равен l*sin(α), где l — длина боковой стороны конуса. В то же время известная по условию задачи высота конуса равна l*cos(α). Из этих равенств легко вывести, что R = h/cos(α)*sin(α) или, что то же самое, R = h*tg(α). Эта формула всегда имеет смысл, поскольку угол α, будучи острым углом прямоугольного треугольника, всегда будет меньше 90°.