Как вычислить угол между векторами
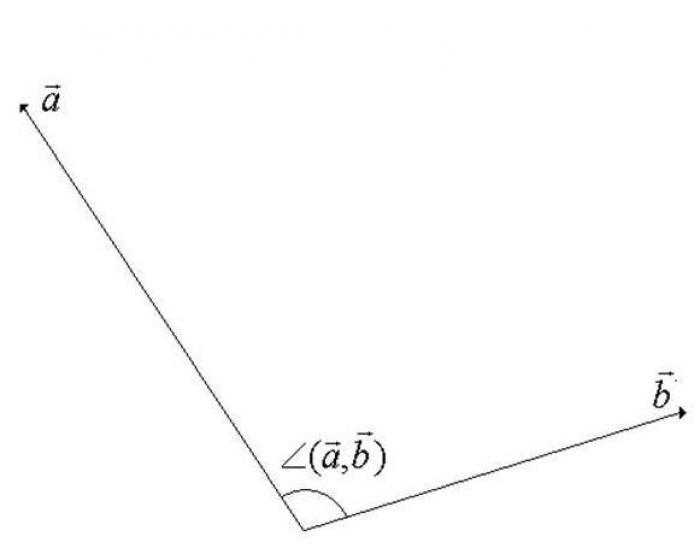
- Вычисление угла между векторами в физике и линейной алгебре
- Определение угла между векторами
- Свойства угла между векторами
- Вычисление угла с использованием скалярного произведения
- Выражение угла между векторами
- Вычисление угла в декартовой системе координат
- Вычисление угла в пространстве
Вычисление угла между векторами в физике и линейной алгебре
Для решения различных задач в физике и линейной алгебре, необходимо уметь вычислять угол между векторами. Однако, эта задача может вызвать множество трудностей, если не понимать сущность скалярного произведения и его результат.
Определение угла между векторами
Угол между векторами в векторном линейном пространстве является минимальным углом, при котором векторы становятся сонаправленными. Для определения угла, один из векторов поворачивается вокруг своей начальной точки. Очевидно, что значение угла не может превышать 180 градусов.
Свойства угла между векторами
При параллельном переносе векторов в линейном пространстве, угол между ними не изменяется. Поэтому для аналитического расчета угла, пространственная ориентация векторов не имеет значения.
Вычисление угла с использованием скалярного произведения
Для вычисления угла между векторами используется определение скалярного произведения. Скалярное произведение векторов представляет собой число или скаляр. Формула для вычисления скалярного произведения векторов на плоскости или в пространстве имеет следующий вид.
Выражение угла между векторами
Данное выражение справедливо только для ненулевых векторов. Из выражения скалярного произведения, можно выразить угол между векторами.
Вычисление угла в декартовой системе координат
Если система координат, в которой располагаются векторы, является декартовой, то выражение для определения угла можно записать в другом виде.
Вычисление угла в пространстве
Если вектора располагаются в пространстве, то расчет угла производится аналогично. Единственным отличием будет появление третьего слагаемого в делимом, которое отвечает за аппликату, то есть третью компоненту вектора. При вычислении модуля векторов, также необходимо учесть компоненту z. Таким образом, для векторов, расположенных в пространстве, выражение для определения угла будет преобразовываться.






