пределы: как их посчитать
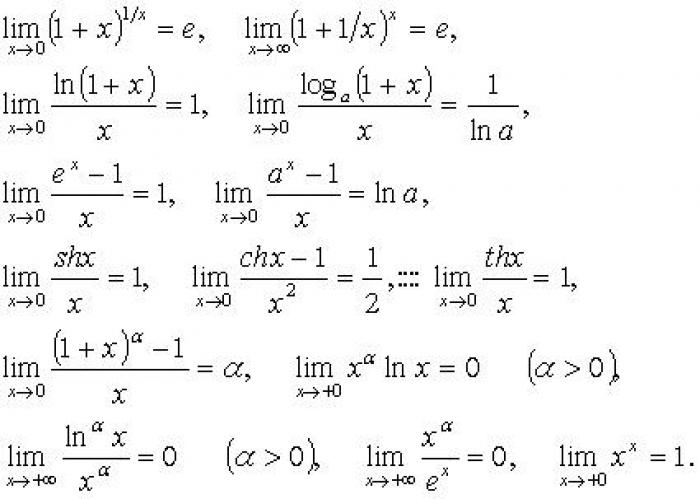
- Значение пределов в математическом анализе
- Пределы и их свойства
- Примеры задач на пределы
- Неопределенности и правила Лопиталя
Значение пределов в математическом анализе
Значение любого выражения стремится к какому-либо пределу, который является постоянным. В курсе математического анализа задачи на пределы встречаются очень часто. Решение этих задач требует определенных знаний и навыков.
Пределы и их свойства
Пределом называется число, к которому стремится переменная или значение выражения. Обычно переменные или функции стремятся либо к нулю, либо к бесконечности. Если предел равен нулю, то величина считается бесконечно малой. Бесконечно малыми называются величины, которые приближаются к нулю. Если предел стремится к бесконечности, то его называют бесконечным пределом.
У пределов есть ряд свойств, некоторые из которых являются аксиомами. Основные свойства пределов включают в себя:
- каждая величина имеет только один предел;
- предел постоянной величины равен самой постоянной;
- предел суммы равен сумме пределов;
- предел произведения равен произведению пределов;
- постоянный множитель может быть вынесен за знак предела;
- предел частного равен частному пределов.
Примеры задач на пределы
В задачах с пределами могут встречаться как числовые выражения, так и производные этих выражений. Примером несложного предела может служить выражение lim 3n + 1 / n + 1 при n стремящемся к бесконечности. Для решения этого предела нужно разделить выражение на n единиц. Известно, что предел 1/n при n стремящемся к бесконечности равен нулю. Поделив пример на n, получаем ответ: lim 3 + 1/n / 1 + 1/n = 3.
Неопределенности и правила Лопиталя
При решении задач на пределы могут возникать результаты, которые называются неопределенностями. Для решения таких случаев применяют правила Лопиталя. Повторное дифференцирование функции позволяет привести пример к форме, в которой его можно решить. Существуют два типа неопределенностей: 0/0 и ∞/∞. Пример с неопределенностью может выглядеть, например, следующим образом: lim 1 - cosx / 4x^2 = (0/0) = lim sinx / 8x = (0/0) = lim cosx / 8 = 1/8x.
Вторым видом неопределенности является ∞/∞. Она часто встречается при решении логарифмов. Примером предела с неопределенностью ∞/∞ может служить выражение lim lnx / sinx = (∞/∞) = lim 1/x / cosx = 0 при x стремящемся к бесконечности.