Как научиться делить в столбик
- Процесс деления в столбик
- Алгоритм деления в столбик
- Подготовка к делению
- Деление без остатка
- Для примера рассмотрим деление числа 1265 на 55 без остатка.
- Деление с остатком
- Для примера рассмотрим деление числа 1276 на 55 с остатком.
- Деление в столбик десятичных дробей
Процесс деления в столбик
Процесс деления в столбик заключается в последовательном выполнении элементарных арифметических действий. Для того чтобы научиться делить в столбик, нужно просто поупражняться в этом несколько раз.
Алгоритм деления в столбик
Алгоритм деления в столбик рассмотрим на следующих примерах - разделим в столбик целые числа без остатка, с остатком и дробные числа, представленные в виде десятичной дроби.
Подготовка к делению
Для выполнения деления в столбик вам понадобится ручка или карандаш и лист бумаги в клетку.
Деление без остатка
Для примера рассмотрим деление числа 1265 на 55 без остатка.
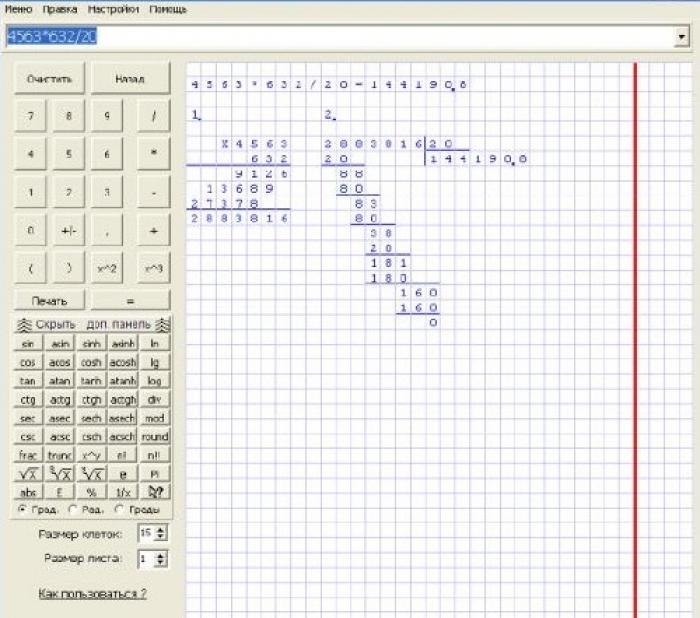
1. Проведите вниз короткую вертикальную линию, высотой в несколько клеток. От этой линии проведите перпендикуляр вправо. Получилась буква «Т», заваленная на левый бок. Над горизонтальной частью заваленной буквы «Т» пишется делитель (55), а слева от него в этой же строчке, за вертикальной частью буквы «Т» – делимое (1265).
2. Определите, какая часть делимого (отсчет идет слева направо по старшинству разрядов) делится на делитель. В данном случае, число 126 является неполным делимым.
3. Прикиньте в уме, на какое число N нужно умножить делитель, чтобы получилось число равное или максимально приближенное (но не большее) к величине неполного делимого. В данном случае, число 2 умноженное на 55 равно 110, что является максимально приближенным числом к 126. Записываем это число под делителем.
4. Умножьте 2 на 55 и запишите полученное число 110 строго под цифрами неполного делимого – слева направо: 1 под 1, 1 под 2 и 0 под 6. Сверху 126, снизу 110. Проведите под 110 короткую горизонтальную черту.
5. Вычтите из 126 число 110. Получится 16. Число 16 – это остаток, который должен быть меньше делителя.
6. Снесите следующую цифру делимого (цифра 5) и запишите ее справа от числа 16. Получилось 165.
7. Повторите действия третьего шага для отношения 165 к 55, то есть найдите число Q, при умножении делителя на которое, получается число максимально приближенное к 165 (но не большее его). В данном случае, число 3 умноженное на 55 равно 165, что является максимально приближенным числом к 165. Запишите цифру 3 справа от цифры 2 под чертой, проведенной под делителем. Это и есть ответ: частное отношения 1265 к 55 равно 23.
Деление с остатком
Для примера рассмотрим деление числа 1276 на 55 с остатком.
1. Повторите все те же действия, что и при делении без остатка. Число N по-прежнему равно 2, но разница между 127 и 110 равна 17.
2. Сносим 6 и определяем число Q. Оно также по-прежнему равно 3, но теперь появляется остаток: 176 – 165 = 11. Остаток 11 меньше 55, вроде бы все нормально. Но сносить-то больше нечего…
3. Допишите справа от делимого ноль и поставьте запятую после цифры 3 в частном. Получается ответ - 23,2. Если бы снесенного в предыдущем шаге нуля не хватило бы для того, чтобы остаток с дописанным нулем оказался больше делителя, нужно было бы дописать еще один ноль в делимом и поставить 0 в частном после запятой (получилось бы 23,0...).
Деление в столбик десятичных дробей
Для деления в столбик десятичных дробей перенесите запятую на одинаковое количество знаков вправо в делимом и делителе так, чтобы и там, и там были целые числа. Дальше – алгоритм деления тот же. Записывайте все числа строго друг под другом согласно изложенным рекомендациям – это не даст возможности допустить ошибку в ходе выполнения расчетов.