Как вычислить матрицу 5 порядка
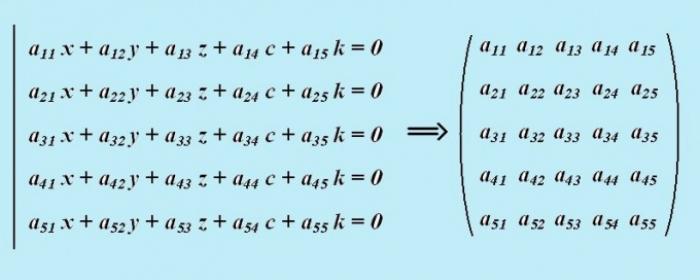
- Матрица и ее определитель
- Вычисление определителя матрицы 5 порядка
- Поиск определителей матриц 4 порядка
- Вычисление определителей матриц 3 порядка
- Нахождение дополнительного минора матрицы 5 порядка
- Вычисление определителя матрицы 5 порядка
Матрица и ее определитель
Матрица - это упорядоченная совокупность чисел в прямоугольной таблице размерности m строк на n столбцов. Определитель матрицы является важным понятием при решении сложных систем линейных уравнений. Для вычисления определителя матрицы различной размерности существует метод разложения по строке или столбцу.
Вычисление определителя матрицы 5 порядка
Инструкция 1: Для вычисления определителя матрицы размерностью 5х5 необходимо провести разложение элементов по первой строке. Возьмите первый элемент этой строки и вычеркните из матрицы строку и столбец, на пересечении которых он находится. Запишите произведение этого элемента на определитель полученной матрицы 4 порядка.
Поиск определителей матриц 4 порядка
Аналогичным образом, последовательно вычеркивайте столбец и строку, содержащие элементы 2, 3, 4 и 5 первой строки начальной матрицы. Для каждого из этих элементов найдите соответствующую матрицу 4х4 и вычислите ее определитель. Умножьте каждый элемент первой строки начальной матрицы на соответствующий дополнительный минор.
Вычисление определителей матриц 3 порядка
Для дальнейшего снижения размерности, найдите определители полученных матриц 4 порядка. Примените тот же метод разложения по строке или столбцу. Умножьте каждый элемент полученной матрицы 3х3 на соответствующие элементы этой же матрицы, используя специальную формулу.
Нахождение дополнительного минора матрицы 5 порядка
Для нахождения дополнительного минора матрицы 5 порядка, воспользуйтесь формулой разложения по строке. Запишите выражение, в котором произведения элементов первой строки матрицы 4 порядка умножаются на соответствующие определители матриц 3 порядка.
Вычисление определителя матрицы 5 порядка
Вычислите оставшиеся слагаемые определителя матрицы 5 порядка, аналогичным образом понижая размерность каждой матрицы 4 порядка. Итоговая формула для вычисления определителя матрицы 5 порядка выглядит следующим образом: Det A = a11*detM1 - a12*detM2 + a13*detM3 - a14*detM4 + a15*detM5.