Как умножить квадратный корень на квадратный корень
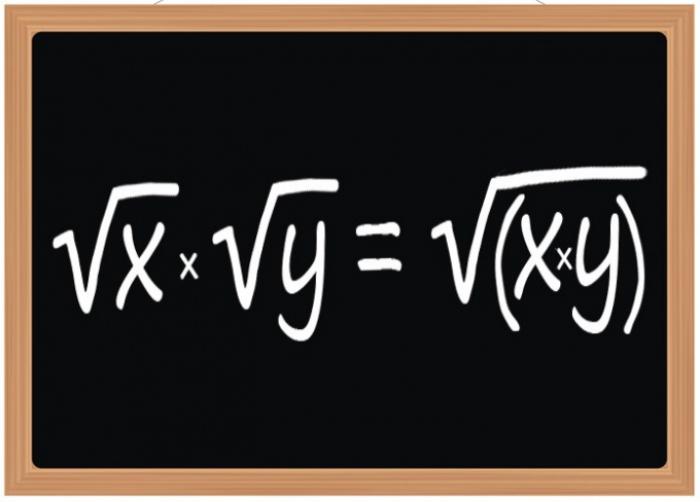
- Умножение и корни
- Правило умножения квадратных корней
- Примеры умножения корней
- Умножение нескольких корней
Умножение и корни
Одна из четырех простейших математических операций, а именно умножение, породила другую операцию - возведение в степень. Последняя в свою очередь добавила дополнительную сложность в обучение математике, породив обратную себе операцию - извлечение корня. Каким-то образом, все эти операции нужно упорядочить, чтобы понять их правила и применение.
Правило умножения квадратных корней
Для умножения квадратных корней существует правило, которое гласит, что результатом этой операции должен стать квадратный корень, подкоренным выражением которого будет произведение подкоренных выражений корней-множителей. Это правило действует при умножении двух, трех и любого другого числа квадратных корней. Однако оно относится не только к корням квадратным, но и к кубическим или с любым другим показателем степени, если этот показатель одинаков у всех участвующих в операции радикалов.
Примеры умножения корней
Инструкция к умножению корней предлагает несколько примеров, которые помогут понять применение правила. Если под знаками умножаемых корней стоят численные значения, то перемножаются сами числа, а полученная величина ставится под знак корня. Например, при умножении корней из чисел 3,14 и 7,62, результат можно записать так: √3,14 * √7,62 = √(3,14*7,62) = √23,9268.
Если подкоренные выражения содержат переменные, то сначала записывается их произведение под одним знаком радикала. Затем полученное подкоренное выражение упрощается. Например, чтобы умножить корень из выражений (x+7) и (x-14), операцию можно записать так: √(x+7) * √(x-14) = √((x+7) * (x-14)) = √(x²-14*x+7*x-7*14) = √(x²-7*x-98).
Умножение нескольких корней
Если необходимо перемножить больше двух квадратных корней, то действуют аналогично - собирают под одним знаком радикала подкоренные выражения всех умножаемых корней в качестве множителей одного сложного выражения. Затем полученное выражение упрощается. Например, при перемножении корней чисел 3,14, 7,62 и 5,56 получаем: √3,14 * √7,62 * √5,56 = √(3,14*7,62*5,56) = √133,033008.
Аналогично, умножение корней, извлекаемых из выражений с переменными x+7, x-14 и 2*x+1, будет выглядеть так: √(x+7) * √(x-14) * √(2*x+1) = √((x+7) * (x-14) * (2*x+1)) = √((x²-14*x+7*x-7*14) * (2*x+1)) = √((x²-7*x-98) * (2*x+1)) = √(2*x*x²-2*x*7*x-2*x*98 + x²-7*x-98) = √(2*x³-14*x²-196*x+x²-7*x-98) = √(2*x³-13*x²-205*x-98).
Таким образом, правила умножения корней помогают упорядочить эту операцию и провести ее правильно, как при численных значениях, так и при использовании переменных.






